Menu Close

Prove-that-8-1-3-4-3-5-4-8-3-5-7-4-8-12-

Tinku Tara 0 Comments
Pin




Question Number 107187 by Dwaipayan Shikari last updated on 09/Aug/20
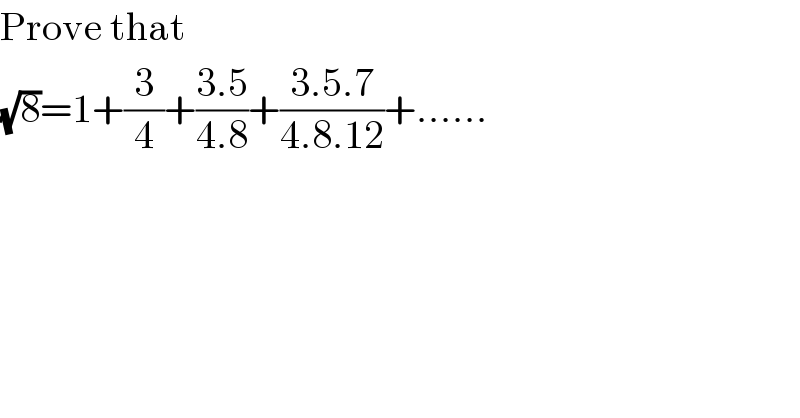
Prove that (√8)=1+(3/4)+((3.5)/(4.8))+((3.5.7)/(4.8.12))+......
$$\mathrm{Prove}\:\mathrm{that} \\ $$$$\sqrt{\mathrm{8}}=\mathrm{1}+\frac{\mathrm{3}}{\mathrm{4}}+\frac{\mathrm{3}.\mathrm{5}}{\mathrm{4}.\mathrm{8}}+\frac{\mathrm{3}.\mathrm{5}.\mathrm{7}}{\mathrm{4}.\mathrm{8}.\mathrm{12}}+…… \\ $$
Commented by john santu last updated on 09/Aug/20
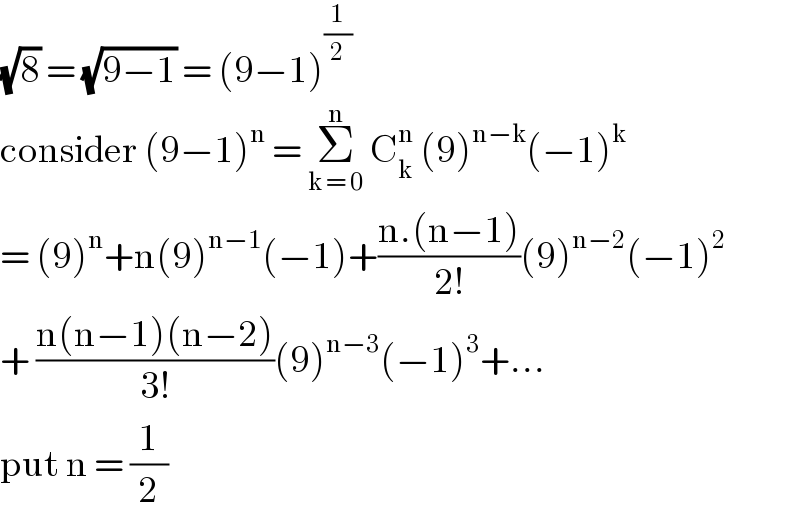
(√8) = (√(9−1)) = (9−1)^(1/2) consider (9−1)^n = Σ_(k = 0) ^n C_k ^n (9)^(n−k) (−1)^k = (9)^n +n(9)^(n−1) (−1)+((n.(n−1))/(2!))(9)^(n−2) (−1)^2 + ((n(n−1)(n−2))/(3!))(9)^(n−3) (−1)^3 +... put n = (1/2)
$$\sqrt{\mathrm{8}}\:=\:\sqrt{\mathrm{9}−\mathrm{1}}\:=\:\left(\mathrm{9}−\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$\mathrm{consider}\:\left(\mathrm{9}−\mathrm{1}\right)^{\mathrm{n}} \:=\:\underset{\mathrm{k}\:=\:\mathrm{0}} {\overset{\mathrm{n}} {\sum}}\:\mathrm{C}_{\mathrm{k}} ^{\mathrm{n}} \:\left(\mathrm{9}\right)^{\mathrm{n}−\mathrm{k}} \left(−\mathrm{1}\right)^{\mathrm{k}} \\ $$$$=\:\left(\mathrm{9}\right)^{\mathrm{n}} +\mathrm{n}\left(\mathrm{9}\right)^{\mathrm{n}−\mathrm{1}} \left(−\mathrm{1}\right)+\frac{\mathrm{n}.\left(\mathrm{n}−\mathrm{1}\right)}{\mathrm{2}!}\left(\mathrm{9}\right)^{\mathrm{n}−\mathrm{2}} \left(−\mathrm{1}\right)^{\mathrm{2}} \\ $$$$+\:\frac{\mathrm{n}\left(\mathrm{n}−\mathrm{1}\right)\left(\mathrm{n}−\mathrm{2}\right)}{\mathrm{3}!}\left(\mathrm{9}\right)^{\mathrm{n}−\mathrm{3}} \left(−\mathrm{1}\right)^{\mathrm{3}} +… \\ $$$$\mathrm{put}\:\mathrm{n}\:=\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by Dwaipayan Shikari last updated on 09/Aug/20
(1+1)^(3/2) =1+(3/2)+(3/8)+(−((3.)/(8.6)))+..(3/(16.24))+... =1+(3/4)+(3/4)+(3/8)−(3/(8.6))+.. =1+(3/4)+((3.12)/(4.8))−(3/(8.6))+. =1+(3/4)+((3.5)/(4.8))+(7/(4.8))−(3/(8.6))+.. = 1+(3/4)+((3.5)/(4.8))+((30)/(4.8.6))+(3/(16.24))+.. = 1+(3/4)+((3.5)/(4.8))+((3.5.4)/(4.8.12))+(3/(16.24))+.. = 1+(3/4)+((3.5)/(4.8))+((3.5.7)/(4.8.12))−((3.5.3)/(4.8.6))+(3/(16.24))+... =1+(3/4)+((3.5)/(4.8))+((3.5.7)/(4.8.12))+.....+C
$$\left(\mathrm{1}+\mathrm{1}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} =\mathrm{1}+\frac{\mathrm{3}}{\mathrm{2}}+\frac{\mathrm{3}}{\mathrm{8}}+\left(−\frac{\mathrm{3}.}{\mathrm{8}.\mathrm{6}}\right)+..\frac{\mathrm{3}}{\mathrm{16}.\mathrm{24}}+… \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{1}+\frac{\mathrm{3}}{\mathrm{4}}+\frac{\mathrm{3}}{\mathrm{4}}+\frac{\mathrm{3}}{\mathrm{8}}−\frac{\mathrm{3}}{\mathrm{8}.\mathrm{6}}+.. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{1}+\frac{\mathrm{3}}{\mathrm{4}}+\frac{\mathrm{3}.\mathrm{12}}{\mathrm{4}.\mathrm{8}}−\frac{\mathrm{3}}{\mathrm{8}.\mathrm{6}}+. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{1}+\frac{\mathrm{3}}{\mathrm{4}}+\frac{\mathrm{3}.\mathrm{5}}{\mathrm{4}.\mathrm{8}}+\frac{\mathrm{7}}{\mathrm{4}.\mathrm{8}}−\frac{\mathrm{3}}{\mathrm{8}.\mathrm{6}}+.. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\:\mathrm{1}+\frac{\mathrm{3}}{\mathrm{4}}+\frac{\mathrm{3}.\mathrm{5}}{\mathrm{4}.\mathrm{8}}+\frac{\mathrm{30}}{\mathrm{4}.\mathrm{8}.\mathrm{6}}+\frac{\mathrm{3}}{\mathrm{16}.\mathrm{24}}+.. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\:\mathrm{1}+\frac{\mathrm{3}}{\mathrm{4}}+\frac{\mathrm{3}.\mathrm{5}}{\mathrm{4}.\mathrm{8}}+\frac{\mathrm{3}.\mathrm{5}.\mathrm{4}}{\mathrm{4}.\mathrm{8}.\mathrm{12}}+\frac{\mathrm{3}}{\mathrm{16}.\mathrm{24}}+.. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{1}+\frac{\mathrm{3}}{\mathrm{4}}+\frac{\mathrm{3}.\mathrm{5}}{\mathrm{4}.\mathrm{8}}+\frac{\mathrm{3}.\mathrm{5}.\mathrm{7}}{\mathrm{4}.\mathrm{8}.\mathrm{12}}−\frac{\mathrm{3}.\mathrm{5}.\mathrm{3}}{\mathrm{4}.\mathrm{8}.\mathrm{6}}+\frac{\mathrm{3}}{\mathrm{16}.\mathrm{24}}+… \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{1}+\frac{\mathrm{3}}{\mathrm{4}}+\frac{\mathrm{3}.\mathrm{5}}{\mathrm{4}.\mathrm{8}}+\frac{\mathrm{3}.\mathrm{5}.\mathrm{7}}{\mathrm{4}.\mathrm{8}.\mathrm{12}}+…..+\mathrm{C} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$
Commented by ZiYangLee last updated on 10/Aug/20
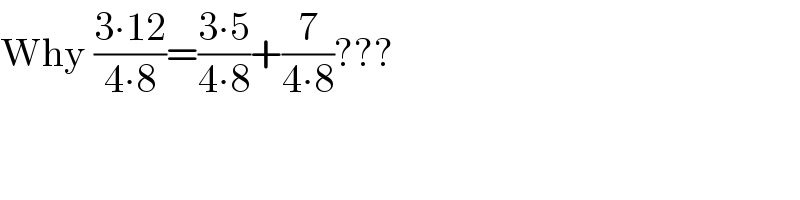
Why ((3∙12)/(4∙8))=((3∙5)/(4∙8))+(7/(4∙8))???
$$\mathrm{Why}\:\frac{\mathrm{3}\centerdot\mathrm{12}}{\mathrm{4}\centerdot\mathrm{8}}=\frac{\mathrm{3}\centerdot\mathrm{5}}{\mathrm{4}\centerdot\mathrm{8}}+\frac{\mathrm{7}}{\mathrm{4}\centerdot\mathrm{8}}??? \\ $$
Answered by ZiYangLee last updated on 10/Aug/20
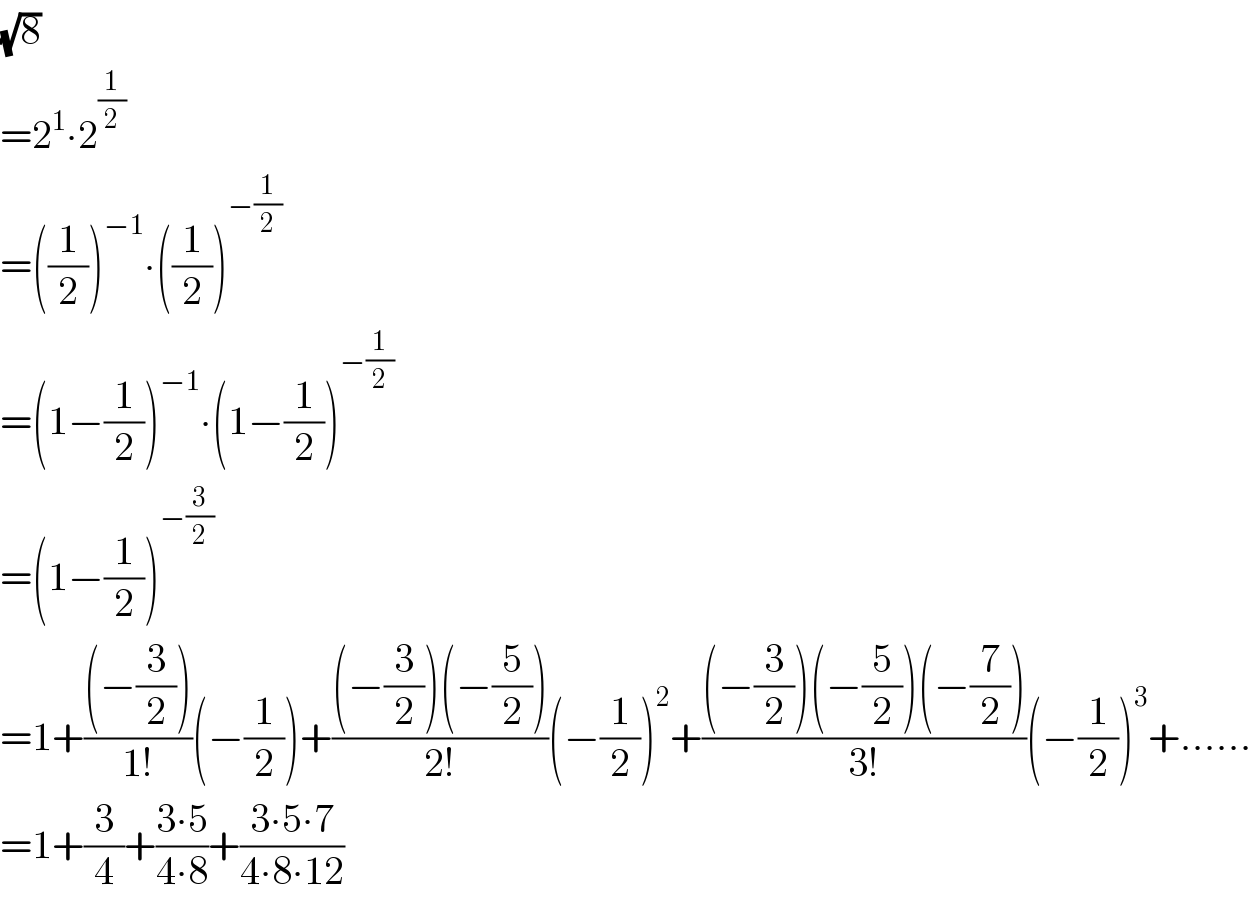
(√8) =2^1 ∙2^(1/2) =((1/2))^(−1) ∙((1/2))^(−(1/2)) =(1−(1/2))^(−1) ∙(1−(1/2))^(−(1/2)) =(1−(1/2))^(−(3/2)) =1+(((−(3/2)))/(1!))(−(1/2))+(((−(3/2))(−(5/2)))/(2!))(−(1/2))^2 +(((−(3/2))(−(5/2))(−(7/2)))/(3!))(−(1/2))^3 +...... =1+(3/4)+((3∙5)/(4∙8))+((3∙5∙7)/(4∙8∙12))
$$\sqrt{\mathrm{8}} \\ $$$$=\mathrm{2}^{\mathrm{1}} \centerdot\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$=\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{−\mathrm{1}} \centerdot\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$=\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{−\mathrm{1}} \centerdot\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$=\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{−\frac{\mathrm{3}}{\mathrm{2}}} \\ $$$$=\mathrm{1}+\frac{\left(−\frac{\mathrm{3}}{\mathrm{2}}\right)}{\mathrm{1}!}\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)+\frac{\left(−\frac{\mathrm{3}}{\mathrm{2}}\right)\left(−\frac{\mathrm{5}}{\mathrm{2}}\right)}{\mathrm{2}!}\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\left(−\frac{\mathrm{3}}{\mathrm{2}}\right)\left(−\frac{\mathrm{5}}{\mathrm{2}}\right)\left(−\frac{\mathrm{7}}{\mathrm{2}}\right)}{\mathrm{3}!}\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{3}} +…… \\ $$$$=\mathrm{1}+\frac{\mathrm{3}}{\mathrm{4}}+\frac{\mathrm{3}\centerdot\mathrm{5}}{\mathrm{4}\centerdot\mathrm{8}}+\frac{\mathrm{3}\centerdot\mathrm{5}\centerdot\mathrm{7}}{\mathrm{4}\centerdot\mathrm{8}\centerdot\mathrm{12}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *