prove-that-any-real-root-of-the-equation-x-6n-4x-2n-4-n-N-0-verify-gt-2-1-2n-

Question Number 150883 by mathdanisur last updated on 16/Aug/21

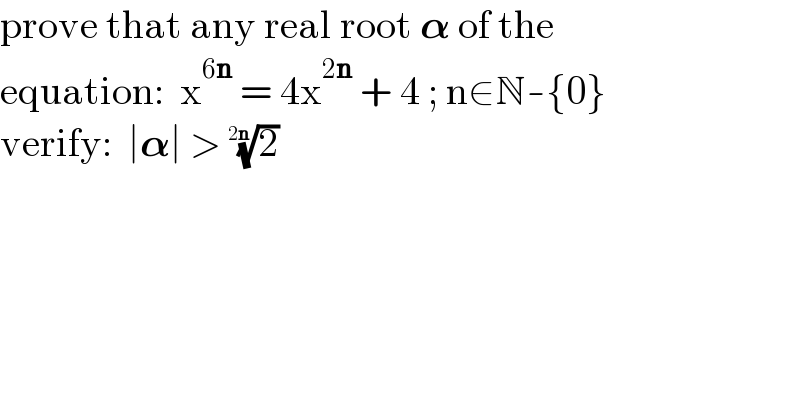
$$\mathrm{prove}\:\mathrm{that}\:\mathrm{any}\:\mathrm{real}\:\mathrm{root}\:\boldsymbol{\alpha}\:\mathrm{of}\:\mathrm{the} \\ $$$$\mathrm{equation}:\:\:\mathrm{x}^{\mathrm{6}\boldsymbol{\mathrm{n}}} \:=\:\mathrm{4x}^{\mathrm{2}\boldsymbol{\mathrm{n}}} \:+\:\mathrm{4}\:;\:\mathrm{n}\in\mathbb{N}-\left\{\mathrm{0}\right\} \\ $$$$\mathrm{verify}:\:\:\mid\boldsymbol{\alpha}\mid\:>\:\sqrt[{\mathrm{2}\boldsymbol{\mathrm{n}}}]{\mathrm{2}} \\ $$

Answered by mindispower last updated on 16/Aug/21

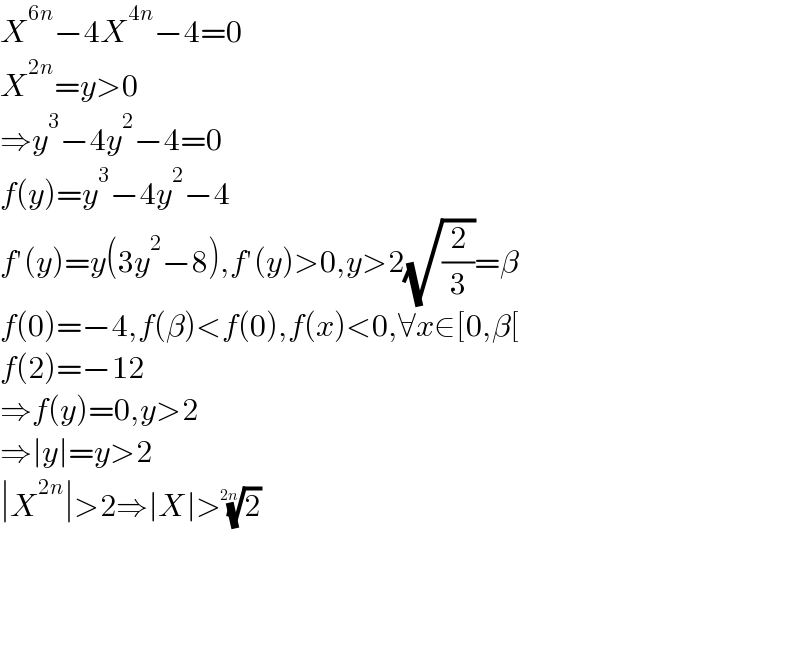
$${X}^{\mathrm{6}{n}} −\mathrm{4}{X}^{\mathrm{4}{n}} −\mathrm{4}=\mathrm{0} \\ $$$${X}^{\mathrm{2}{n}} ={y}>\mathrm{0} \\ $$$$\Rightarrow{y}^{\mathrm{3}} −\mathrm{4}{y}^{\mathrm{2}} −\mathrm{4}=\mathrm{0} \\ $$$${f}\left({y}\right)={y}^{\mathrm{3}} −\mathrm{4}{y}^{\mathrm{2}} −\mathrm{4} \\ $$$${f}'\left({y}\right)={y}\left(\mathrm{3}{y}^{\mathrm{2}} −\mathrm{8}\right),{f}'\left({y}\right)>\mathrm{0},{y}>\mathrm{2}\sqrt{\frac{\mathrm{2}}{\mathrm{3}}}=\beta \\ $$$${f}\left(\mathrm{0}\right)=−\mathrm{4},{f}\left(\beta\right)<{f}\left(\mathrm{0}\right),{f}\left({x}\right)<\mathrm{0},\forall{x}\in\left[\mathrm{0},\beta\left[\right.\right. \\ $$$${f}\left(\mathrm{2}\right)=−\mathrm{12} \\ $$$$\Rightarrow{f}\left({y}\right)=\mathrm{0},{y}>\mathrm{2} \\ $$$$\Rightarrow\mid{y}\mid={y}>\mathrm{2} \\ $$$$\mid{X}^{\mathrm{2}{n}} \mid>\mathrm{2}\Rightarrow\mid{X}\mid>\sqrt[{\mathrm{2}{n}}]{\mathrm{2}} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Commented by mathdanisur last updated on 16/Aug/21

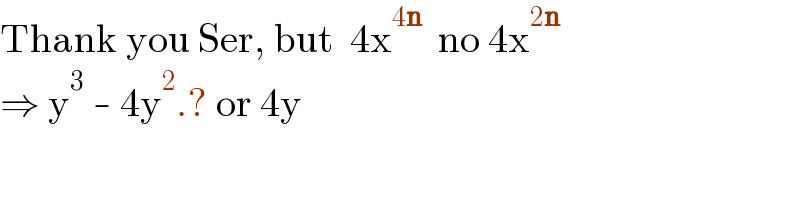
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{Ser},\:\mathrm{but}\:\:\mathrm{4x}^{\mathrm{4}\boldsymbol{\mathrm{n}}} \:\:\mathrm{no}\:\mathrm{4x}^{\mathrm{2}\boldsymbol{\mathrm{n}}} \\ $$$$\Rightarrow\:\mathrm{y}^{\mathrm{3}} \:-\:\mathrm{4y}^{\mathrm{2}} .?\:\mathrm{or}\:\mathrm{4y} \\ $$

Terms of Service
Privacy Policy
Contact: info@tinkutara.com