Question Number 38112 by maxmathsup by imad last updated on 21/Jun/18
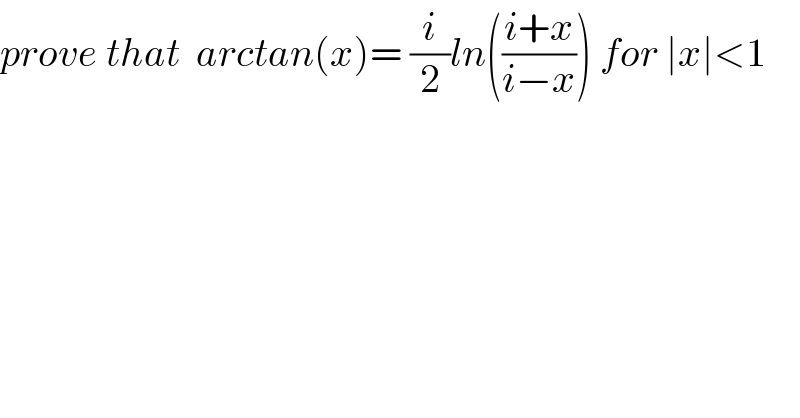
$${prove}\:{that}\:\:{arctan}\left({x}\right)=\:\frac{{i}}{\mathrm{2}}{ln}\left(\frac{{i}+{x}}{{i}−{x}}\right)\:{for}\:\mid{x}\mid<\mathrm{1} \\ $$
Commented by prof Abdo imad last updated on 24/Jun/18
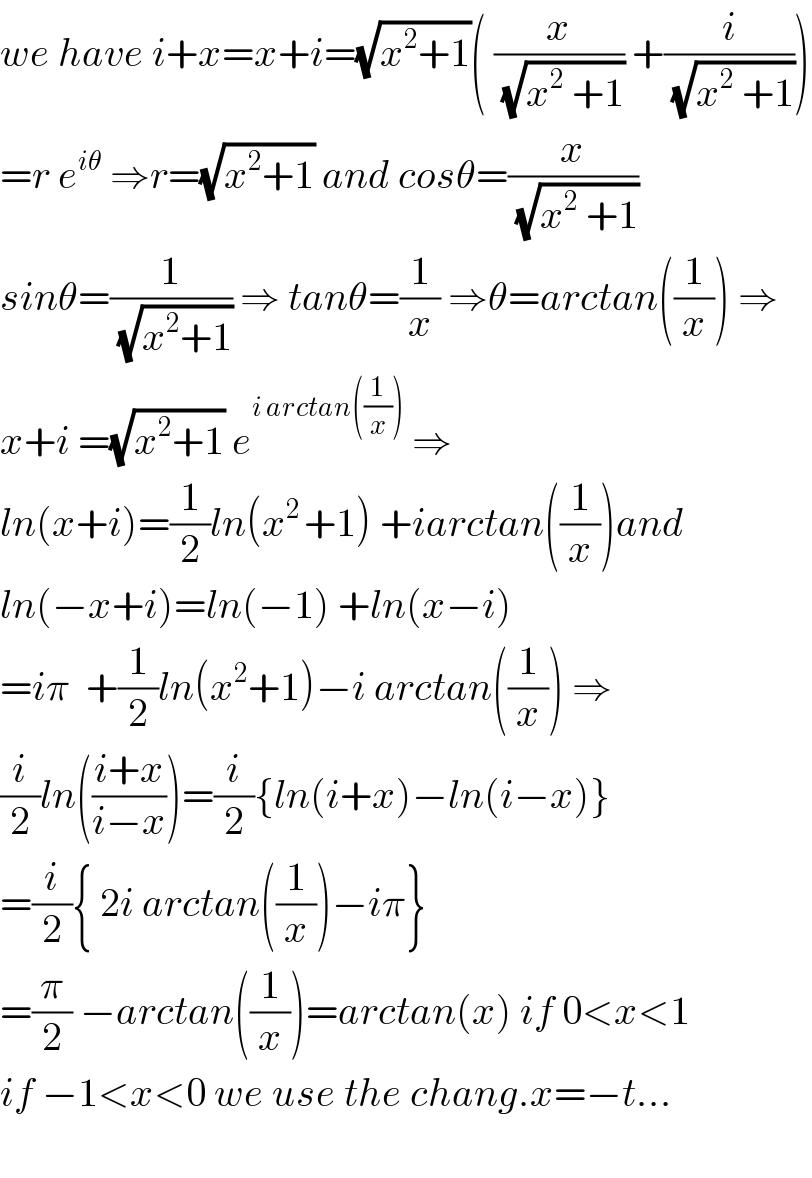
$${we}\:{have}\:{i}+{x}={x}+{i}=\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\left(\:\frac{{x}}{\:\sqrt{{x}^{\mathrm{2}} \:+\mathrm{1}}}\:+\frac{{i}}{\:\sqrt{{x}^{\mathrm{2}} \:+\mathrm{1}}}\right) \\ $$$$={r}\:{e}^{{i}\theta} \:\Rightarrow{r}=\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\:{and}\:{cos}\theta=\frac{{x}}{\:\sqrt{{x}^{\mathrm{2}} \:+\mathrm{1}}} \\ $$$${sin}\theta=\frac{\mathrm{1}}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}\:\Rightarrow\:{tan}\theta=\frac{\mathrm{1}}{{x}}\:\Rightarrow\theta={arctan}\left(\frac{\mathrm{1}}{{x}}\right)\:\Rightarrow \\ $$$${x}+{i}\:=\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\:{e}^{{i}\:{arctan}\left(\frac{\mathrm{1}}{{x}}\right)} \:\Rightarrow \\ $$$${ln}\left({x}+{i}\right)=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left({x}^{\mathrm{2}\:} +\mathrm{1}\right)\:+{iarctan}\left(\frac{\mathrm{1}}{{x}}\right){and} \\ $$$${ln}\left(−{x}+{i}\right)={ln}\left(−\mathrm{1}\right)\:+{ln}\left({x}−{i}\right) \\ $$$$={i}\pi\:\:+\frac{\mathrm{1}}{\mathrm{2}}{ln}\left({x}^{\mathrm{2}} +\mathrm{1}\right)−{i}\:{arctan}\left(\frac{\mathrm{1}}{{x}}\right)\:\Rightarrow \\ $$$$\frac{{i}}{\mathrm{2}}{ln}\left(\frac{{i}+{x}}{{i}−{x}}\right)=\frac{{i}}{\mathrm{2}}\left\{{ln}\left({i}+{x}\right)−{ln}\left({i}−{x}\right)\right\} \\ $$$$=\frac{{i}}{\mathrm{2}}\left\{\:\mathrm{2}{i}\:{arctan}\left(\frac{\mathrm{1}}{{x}}\right)−{i}\pi\right\} \\ $$$$=\frac{\pi}{\mathrm{2}}\:−{arctan}\left(\frac{\mathrm{1}}{{x}}\right)={arctan}\left({x}\right)\:{if}\:\mathrm{0}<{x}<\mathrm{1} \\ $$$${if}\:−\mathrm{1}<{x}<\mathrm{0}\:{we}\:{use}\:{the}\:{chang}.{x}=−{t}… \\ $$$$ \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 22/Jun/18
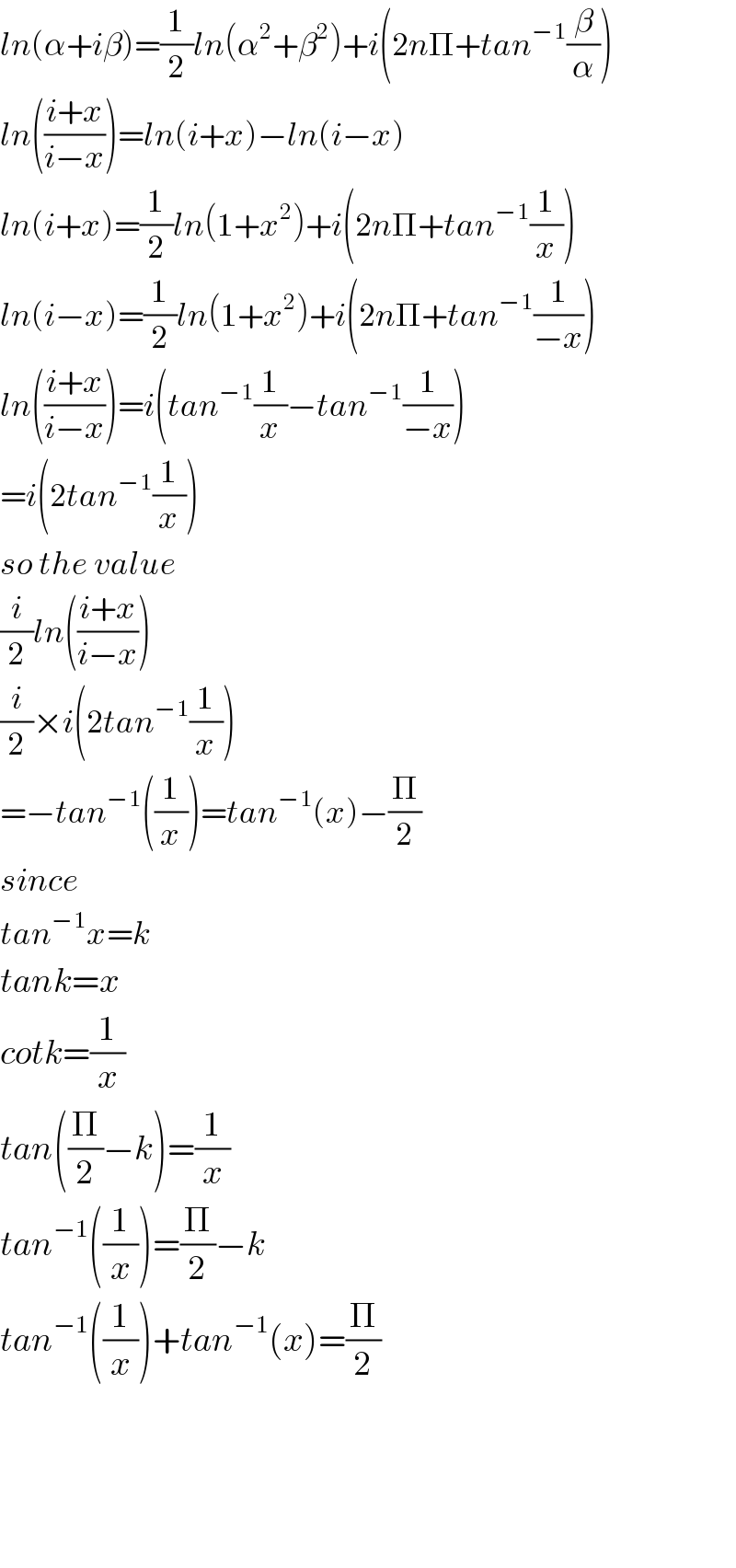
$${ln}\left(\alpha+{i}\beta\right)=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} \right)+{i}\left(\mathrm{2}{n}\Pi+{tan}^{−\mathrm{1}} \frac{\beta}{\alpha}\right) \\ $$$${ln}\left(\frac{{i}+{x}}{{i}−{x}}\right)={ln}\left({i}+{x}\right)−{ln}\left({i}−{x}\right) \\ $$$${ln}\left({i}+{x}\right)=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)+{i}\left(\mathrm{2}{n}\Pi+{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{{x}}\right) \\ $$$${ln}\left({i}−{x}\right)=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)+{i}\left(\mathrm{2}{n}\Pi+{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{−{x}}\right) \\ $$$${ln}\left(\frac{{i}+{x}}{{i}−{x}}\right)={i}\left({tan}^{−\mathrm{1}} \frac{\mathrm{1}}{{x}}−{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{−{x}}\right) \\ $$$$={i}\left(\mathrm{2}{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{{x}}\right) \\ $$$${so}\:{the}\:{value} \\ $$$$\frac{{i}}{\mathrm{2}}{ln}\left(\frac{{i}+{x}}{{i}−{x}}\right) \\ $$$$\frac{{i}}{\mathrm{2}}×{i}\left(\mathrm{2}{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{{x}}\right) \\ $$$$=−{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{{x}}\right)={tan}^{−\mathrm{1}} \left({x}\right)−\frac{\Pi}{\mathrm{2}} \\ $$$${since} \\ $$$${tan}^{−\mathrm{1}} {x}={k} \\ $$$${tank}={x} \\ $$$${cotk}=\frac{\mathrm{1}}{{x}} \\ $$$${tan}\left(\frac{\Pi}{\mathrm{2}}−{k}\right)=\frac{\mathrm{1}}{{x}} \\ $$$${tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{{x}}\right)=\frac{\Pi}{\mathrm{2}}−{k} \\ $$$${tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{{x}}\right)+{tan}^{−\mathrm{1}} \left({x}\right)=\frac{\Pi}{\mathrm{2}} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
