Question Number 151448 by mathdanisur last updated on 21/Aug/21
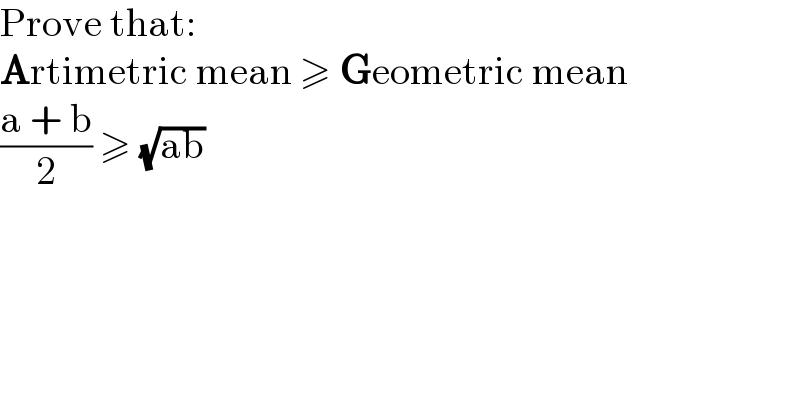
$$\mathrm{Prove}\:\mathrm{that}: \\ $$$$\boldsymbol{\mathrm{A}}\mathrm{rtimetric}\:\mathrm{mean}\:\geqslant\:\boldsymbol{\mathrm{G}}\mathrm{eometric}\:\mathrm{mean} \\ $$$$\frac{\mathrm{a}\:+\:\mathrm{b}}{\mathrm{2}}\:\geqslant\:\sqrt{\mathrm{ab}} \\ $$
Commented by puissant last updated on 21/Aug/21

$$\forall\:\left({a},{b}\right)\in\mathbb{R}^{\mathrm{2}} , \\ $$$$\left(\sqrt{{a}}−\sqrt{{b}}\right)^{\mathrm{2}} \geqslant\mathrm{0} \\ $$$$\Rightarrow\:{a}−\mathrm{2}\sqrt{{ab}}+{b}\geqslant\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{2}\sqrt{{ab}}\leqslant{a}+{b} \\ $$$$\Rightarrow\:\sqrt{{ab}}\:\leqslant\:\frac{{a}+{b}}{\mathrm{2}}.. \\ $$
Commented by mathdanisur last updated on 21/Aug/21

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{Ser} \\ $$
Answered by nimnim last updated on 21/Aug/21
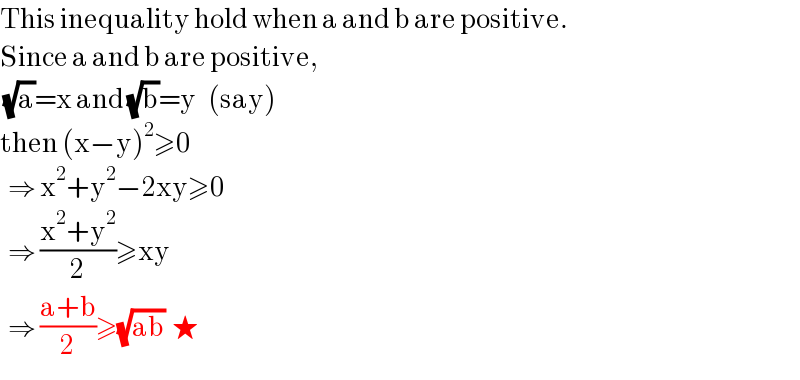
$$\mathrm{This}\:\mathrm{inequality}\:\mathrm{hold}\:\mathrm{when}\:\mathrm{a}\:\mathrm{and}\:\mathrm{b}\:\mathrm{are}\:\mathrm{positive}. \\ $$$$\mathrm{Since}\:\mathrm{a}\:\mathrm{and}\:\mathrm{b}\:\mathrm{are}\:\mathrm{positive}, \\ $$$$\:\sqrt{\mathrm{a}}=\mathrm{x}\:\mathrm{and}\:\sqrt{\mathrm{b}}=\mathrm{y}\:\:\:\left(\mathrm{say}\right) \\ $$$$\mathrm{then}\:\left(\mathrm{x}−\mathrm{y}\right)^{\mathrm{2}} \geqslant\mathrm{0} \\ $$$$\:\:\Rightarrow\:\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} −\mathrm{2xy}\geqslant\mathrm{0} \\ $$$$\:\:\Rightarrow\:\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} }{\mathrm{2}}\geqslant\mathrm{xy} \\ $$$$\:\:\Rightarrow\:\frac{\mathrm{a}+\mathrm{b}}{\mathrm{2}}\geqslant\sqrt{\mathrm{ab}}\:\:\bigstar \\ $$
Commented by mathdanisur last updated on 21/Aug/21

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{Ser} \\ $$
