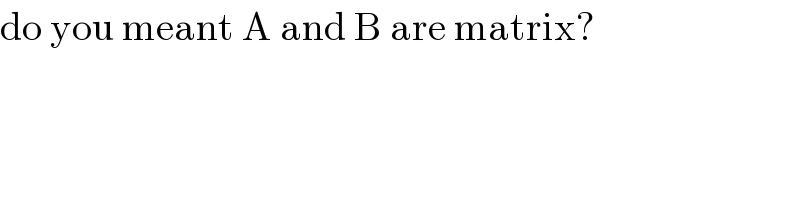prove-that-B-1-A-1-AB-1-if-A-34-12-B-12-13-please-sir-help-me-

Question Number 112906 by mohammad17 last updated on 10/Sep/20

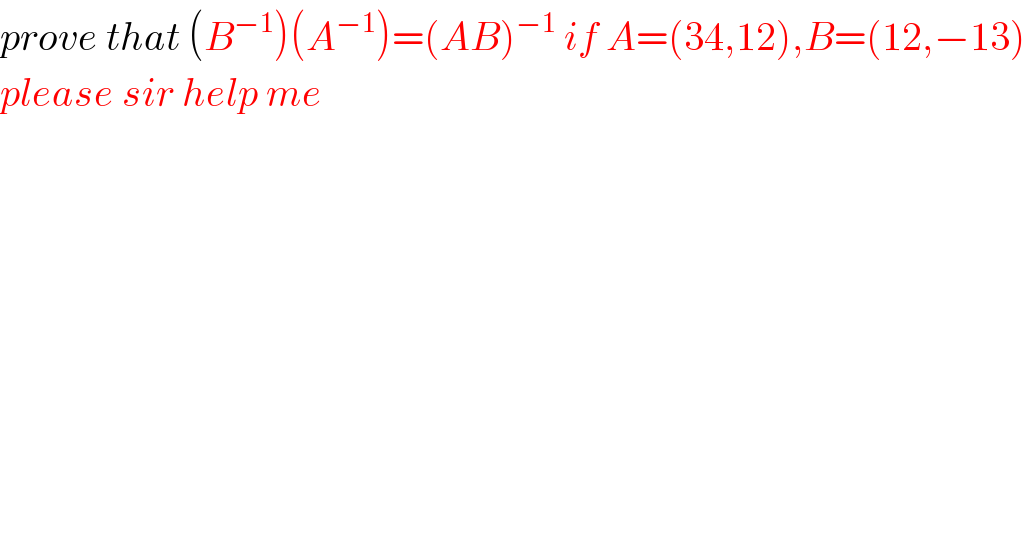
p r o v e t h a t (B^{- 1}) (A^{- 1}) = {(A B)}^{- 1} i f A = (34, 12), B = (12, - 13)

p l e a s e s i r h e l p m e

Commented by mohammad17 last updated on 10/Sep/20

h e l p m e s i r

Commented by mohammad17 last updated on 10/Sep/20

y e s s i r

Commented by kaivan.ahmadi last updated on 10/Sep/20

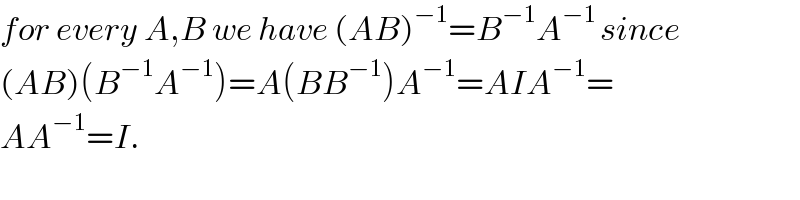
f o r e v e r y A, B w e h a v e {(A B)}^{- 1} = B^{- 1} A^{- 1} s i n c e

(A B) (B^{- 1} A^{- 1}) = A ({B B}^{- 1}) A^{- 1} = {A I A}^{- 1} =

{A A}^{- 1} = I .

Commented by bemath last updated on 10/Sep/20

do you meant A and B are matrix ?

Facebook Tweet Pin