Prove-that-b-2asin-2-when-acos-bsin-c-and-45-

Question Number 26135 by JI Siam last updated on 21/Dec/17

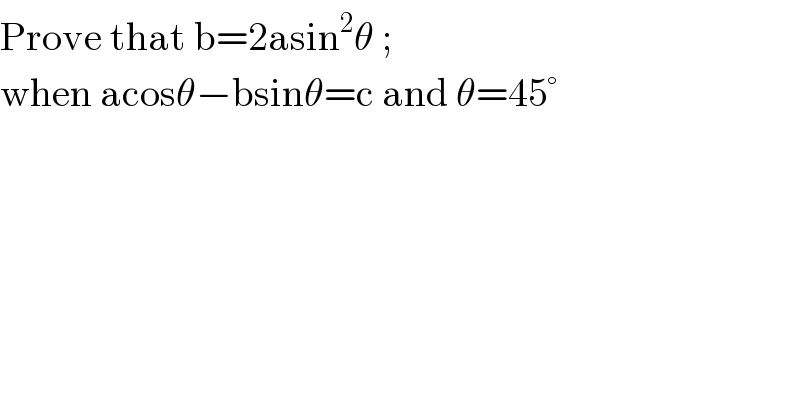
Prove that b = {2 asin}^{2} θ;

when acos θ - bsin θ = c and θ = 45 °

Commented by mrW1 last updated on 21/Dec/17

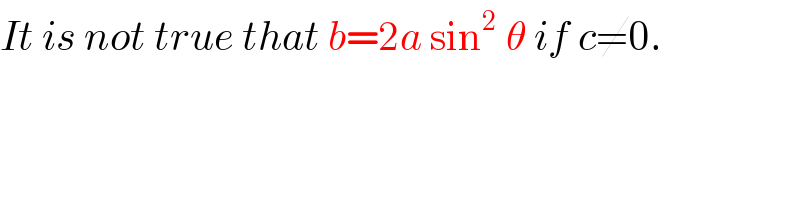
I t i s n o t t r u e t h a t b = 2 a \sin^{2} θ i f c \neq 0 .

Answered by ajfour last updated on 21/Dec/17

b = a t h e n c = 0 .

Facebook Tweet Pin