Question Number 168297 by MdNafiz last updated on 07/Apr/22
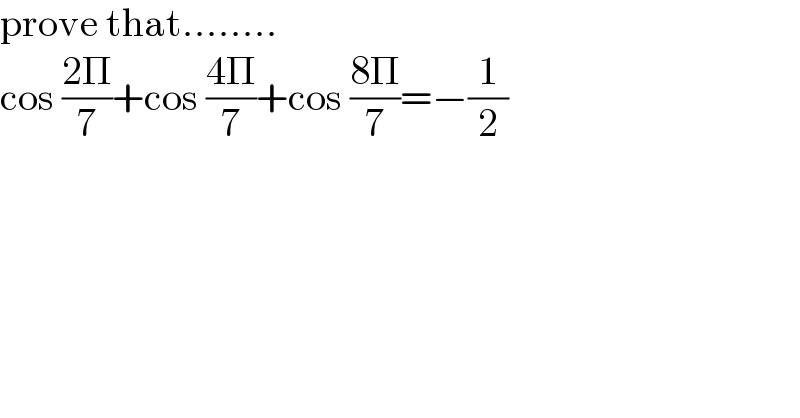
$$\mathrm{prove}\:\mathrm{that}…….. \\ $$$$\mathrm{cos}\:\frac{\mathrm{2}\Pi}{\mathrm{7}}+\mathrm{cos}\:\frac{\mathrm{4}\Pi}{\mathrm{7}}+\mathrm{cos}\:\frac{\mathrm{8}\Pi}{\mathrm{7}}=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Answered by som(math1967) last updated on 07/Apr/22
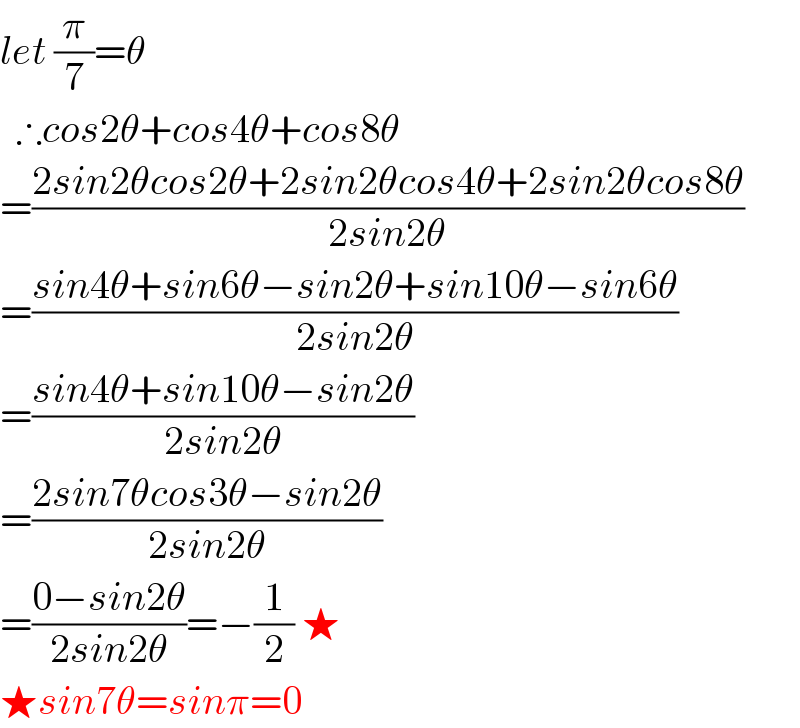
$${let}\:\frac{\pi}{\mathrm{7}}=\theta \\ $$$$\:\:\therefore{cos}\mathrm{2}\theta+{cos}\mathrm{4}\theta+{cos}\mathrm{8}\theta \\ $$$$=\frac{\mathrm{2}{sin}\mathrm{2}\theta{cos}\mathrm{2}\theta+\mathrm{2}{sin}\mathrm{2}\theta{cos}\mathrm{4}\theta+\mathrm{2}{sin}\mathrm{2}\theta{cos}\mathrm{8}\theta}{\mathrm{2}{sin}\mathrm{2}\theta} \\ $$$$=\frac{{sin}\mathrm{4}\theta+{sin}\mathrm{6}\theta−{sin}\mathrm{2}\theta+{sin}\mathrm{10}\theta−{sin}\mathrm{6}\theta}{\mathrm{2}{sin}\mathrm{2}\theta} \\ $$$$=\frac{{sin}\mathrm{4}\theta+{sin}\mathrm{10}\theta−{sin}\mathrm{2}\theta}{\mathrm{2}{sin}\mathrm{2}\theta} \\ $$$$=\frac{\mathrm{2}{sin}\mathrm{7}\theta{cos}\mathrm{3}\theta−{sin}\mathrm{2}\theta}{\mathrm{2}{sin}\mathrm{2}\theta} \\ $$$$=\frac{\mathrm{0}−{sin}\mathrm{2}\theta}{\mathrm{2}{sin}\mathrm{2}\theta}=−\frac{\mathrm{1}}{\mathrm{2}}\:\bigstar \\ $$$$\bigstar{sin}\mathrm{7}\theta={sin}\pi=\mathrm{0} \\ $$
Commented by peter frank last updated on 08/Apr/22

$$\mathrm{good} \\ $$
