Question Number 16598 by Tinkutara last updated on 24/Jun/17
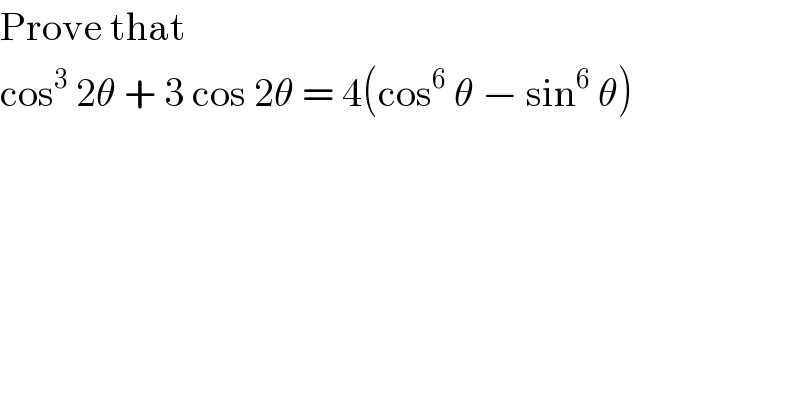
$$\mathrm{Prove}\:\mathrm{that} \\ $$$$\mathrm{cos}^{\mathrm{3}} \:\mathrm{2}\theta\:+\:\mathrm{3}\:\mathrm{cos}\:\mathrm{2}\theta\:=\:\mathrm{4}\left(\mathrm{cos}^{\mathrm{6}} \:\theta\:−\:\mathrm{sin}^{\mathrm{6}} \:\theta\right) \\ $$
Answered by ajfour last updated on 24/Jun/17
![L.H.S. = cos 2θ(cos^2 2θ+3) =cos 2θ[(2cos^2 θ−1)^2 +3] =cos 2θ[ 4cos^4 θ−4cos^2 θ+4] =4cos 2θ[ cos^4 θ+sin^2 θ] =4cos 2θ[ cos^4 θ+(sin^2 θ+cos^2 θ)sin^2 θ] =4(cos^2 θ−sin^2 θ)(cos^4 θ+ cos^2 θ sin^2 θ+sin^4 θ) =4[(cos^2 θ)^3 −(sin^2 θ)^3 ] L.H.S.= 4(cos^6 θ−sin^6 θ)=R.H.S..](https://www.tinkutara.com/question/Q16601.png)
$$\mathrm{L}.\mathrm{H}.\mathrm{S}.\:=\:\mathrm{cos}\:\mathrm{2}\theta\left(\mathrm{cos}\:^{\mathrm{2}} \mathrm{2}\theta+\mathrm{3}\right) \\ $$$$\:=\mathrm{cos}\:\mathrm{2}\theta\left[\left(\mathrm{2cos}\:^{\mathrm{2}} \theta−\mathrm{1}\right)^{\mathrm{2}} +\mathrm{3}\right] \\ $$$$\:=\mathrm{cos}\:\mathrm{2}\theta\left[\:\mathrm{4cos}\:^{\mathrm{4}} \theta−\mathrm{4cos}\:^{\mathrm{2}} \theta+\mathrm{4}\right] \\ $$$$\:=\mathrm{4cos}\:\mathrm{2}\theta\left[\:\mathrm{cos}\:^{\mathrm{4}} \theta+\mathrm{sin}\:^{\mathrm{2}} \theta\right] \\ $$$$\:=\mathrm{4cos}\:\mathrm{2}\theta\left[\:\mathrm{cos}\:^{\mathrm{4}} \theta+\left(\mathrm{sin}\:^{\mathrm{2}} \theta+\mathrm{cos}\:^{\mathrm{2}} \theta\right)\mathrm{sin}\:^{\mathrm{2}} \theta\right] \\ $$$$=\mathrm{4}\left(\mathrm{cos}\:^{\mathrm{2}} \theta−\mathrm{sin}\:^{\mathrm{2}} \theta\right)\left(\mathrm{cos}\:^{\mathrm{4}} \theta+\right. \\ $$$$\left.\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{cos}\:^{\mathrm{2}} \theta\:\mathrm{sin}\:^{\mathrm{2}} \theta+\mathrm{sin}\:^{\mathrm{4}} \theta\right) \\ $$$$=\mathrm{4}\left[\left(\mathrm{cos}\:^{\mathrm{2}} \theta\right)^{\mathrm{3}} −\left(\mathrm{sin}\:^{\mathrm{2}} \theta\right)^{\mathrm{3}} \right] \\ $$$$\mathrm{L}.\mathrm{H}.\mathrm{S}.=\:\mathrm{4}\left(\mathrm{cos}\:^{\mathrm{6}} \theta−\mathrm{sin}\:^{\mathrm{6}} \theta\right)=\mathrm{R}.\mathrm{H}.\mathrm{S}.. \\ $$
Commented by Tinkutara last updated on 24/Jun/17

$$\mathrm{Thanks}\:\mathrm{Sir}! \\ $$
