Question Number 157065 by apriadodir last updated on 19/Oct/21
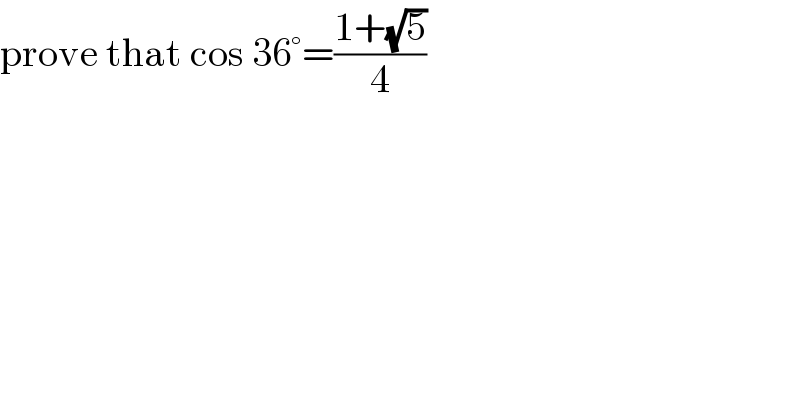
$$\mathrm{prove}\:\mathrm{that}\:\mathrm{cos}\:\mathrm{36}°=\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{4}} \\ $$
Commented by cortano last updated on 19/Oct/21
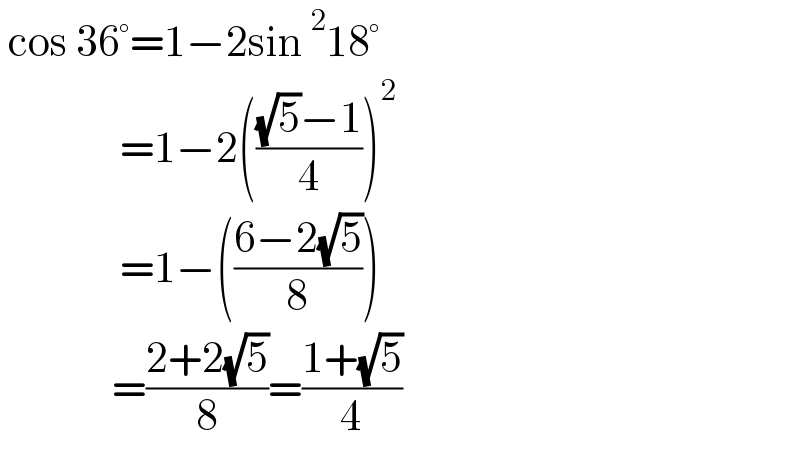
$$\:\mathrm{cos}\:\mathrm{36}°=\mathrm{1}−\mathrm{2sin}\:^{\mathrm{2}} \mathrm{18}° \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{1}−\mathrm{2}\left(\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{4}}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{1}−\left(\frac{\mathrm{6}−\mathrm{2}\sqrt{\mathrm{5}}}{\mathrm{8}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{2}+\mathrm{2}\sqrt{\mathrm{5}}}{\mathrm{8}}=\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{4}} \\ $$
