Question Number 15555 by Tinkutara last updated on 11/Jun/17
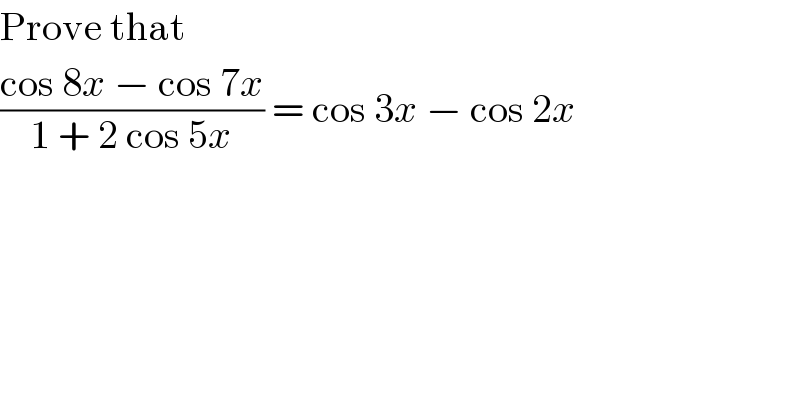
$$\mathrm{Prove}\:\mathrm{that} \\ $$$$\frac{\mathrm{cos}\:\mathrm{8}{x}\:−\:\mathrm{cos}\:\mathrm{7}{x}}{\mathrm{1}\:+\:\mathrm{2}\:\mathrm{cos}\:\mathrm{5}{x}}\:=\:\mathrm{cos}\:\mathrm{3}{x}\:−\:\mathrm{cos}\:\mathrm{2}{x} \\ $$
Answered by ajfour last updated on 11/Jun/17
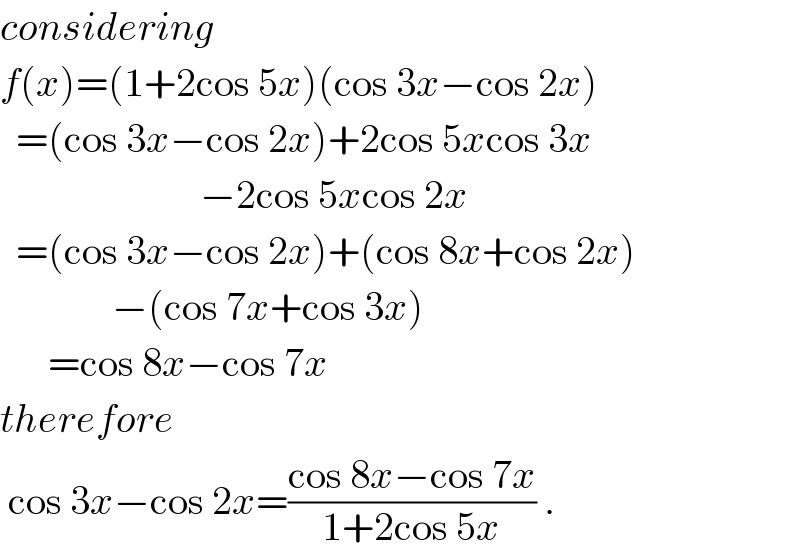
$${considering} \\ $$$${f}\left({x}\right)=\left(\mathrm{1}+\mathrm{2cos}\:\mathrm{5}{x}\right)\left(\mathrm{cos}\:\mathrm{3}{x}−\mathrm{cos}\:\mathrm{2}{x}\right) \\ $$$$\:\:=\left(\mathrm{cos}\:\mathrm{3}{x}−\mathrm{cos}\:\mathrm{2}{x}\right)+\mathrm{2cos}\:\mathrm{5}{x}\mathrm{cos}\:\mathrm{3}{x} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{2cos}\:\mathrm{5}{x}\mathrm{cos}\:\mathrm{2}{x} \\ $$$$\:\:=\left(\mathrm{cos}\:\mathrm{3}{x}−\mathrm{cos}\:\mathrm{2}{x}\right)+\left(\mathrm{cos}\:\mathrm{8}{x}+\mathrm{cos}\:\mathrm{2}{x}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\left(\mathrm{cos}\:\mathrm{7}{x}+\mathrm{cos}\:\mathrm{3}{x}\right) \\ $$$$\:\:\:\:\:\:=\mathrm{cos}\:\mathrm{8}{x}−\mathrm{cos}\:\mathrm{7}{x} \\ $$$${therefore}\: \\ $$$$\:\mathrm{cos}\:\mathrm{3}{x}−\mathrm{cos}\:\mathrm{2}{x}=\frac{\mathrm{cos}\:\mathrm{8}{x}−\mathrm{cos}\:\mathrm{7}{x}}{\mathrm{1}+\mathrm{2cos}\:\mathrm{5}{x}}\:. \\ $$
Commented by Tinkutara last updated on 13/Jun/17

$$\mathrm{Thanks}\:\mathrm{Sir}\:\mathrm{but}\:\mathrm{I}\:\mathrm{needed}\:\mathrm{to}\:\mathrm{prove}\:\mathrm{LHS} \\ $$$$=\:\mathrm{RHS}.\:\mathrm{Can}\:\mathrm{it}\:\mathrm{be}\:\mathrm{done}? \\ $$
