Question Number 103481 by mohammad17 last updated on 15/Jul/20
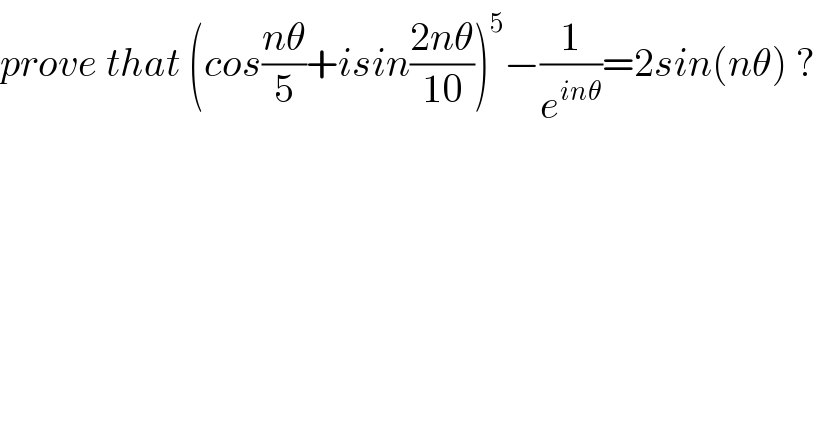
$${prove}\:{that}\:\left({cos}\frac{{n}\theta}{\mathrm{5}}+{isin}\frac{\mathrm{2}{n}\theta}{\mathrm{10}}\right)^{\mathrm{5}} −\frac{\mathrm{1}}{{e}^{{in}\theta} }=\mathrm{2}{sin}\left({n}\theta\right)\:? \\ $$
Answered by Dwaipayan Shikari last updated on 15/Jul/20
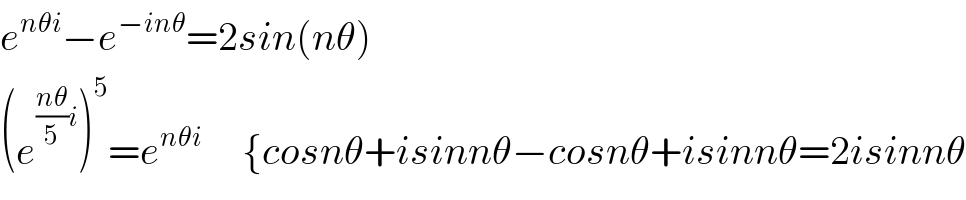
$${e}^{{n}\theta{i}} −{e}^{−{in}\theta} =\mathrm{2}{sin}\left({n}\theta\right) \\ $$$$\left({e}^{\frac{{n}\theta}{\mathrm{5}}{i}} \right)^{\mathrm{5}} ={e}^{{n}\theta{i}} \:\:\:\:\:\left\{{cosn}\theta+{isinn}\theta−{cosn}\theta+{isinn}\theta=\mathrm{2}{isinn}\theta\right. \\ $$
Commented by mohammad17 last updated on 15/Jul/20

$${thank}\:{you}\:{sir} \\ $$
