Menu Close

prove-that-cos-pi-15-cos-2pi-15-cos-3pi-15-cos-4pi-15-cos-5pi-15-cos-6pi-15-cos-7pi-15-1-2-7-

Tinku Tara 0 Comments
Pin




Question Number 37864 by kunal1234523 last updated on 18/Jun/18
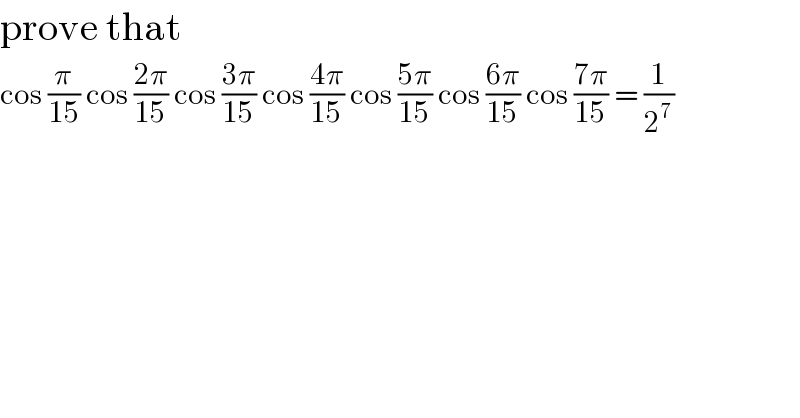
prove that cos (π/(15)) cos ((2π)/(15)) cos ((3π)/(15)) cos ((4π)/(15)) cos ((5π)/(15)) cos ((6π)/(15)) cos ((7π)/(15)) = (1/2^7 )
$$\mathrm{prove}\:\mathrm{that} \\ $$$$\mathrm{cos}\:\frac{\pi}{\mathrm{15}}\:\mathrm{cos}\:\frac{\mathrm{2}\pi}{\mathrm{15}}\:\mathrm{cos}\:\frac{\mathrm{3}\pi}{\mathrm{15}}\:\mathrm{cos}\:\frac{\mathrm{4}\pi}{\mathrm{15}}\:\mathrm{cos}\:\frac{\mathrm{5}\pi}{\mathrm{15}}\:\mathrm{cos}\:\frac{\mathrm{6}\pi}{\mathrm{15}}\:\mathrm{cos}\:\frac{\mathrm{7}\pi}{\mathrm{15}}\:=\:\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{7}} } \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 18/Jun/18
cosx.cos2x.cos3x.cos4x.cos5x.cos6x.cos7x=k x=(Π/(15)) 2sinx.k=(2sinxcosx).cos2x.coz3x.coz4x.cos5x cos6x.cos7x 2^2 sinx.k=(2sin2xcos2x)cos3xcos4xcos5xcos6x cos7x 2^3 sinx.k=(2sin4xcos4x)cos3xcos5xcos6xco7x 2^3 sinx.k=(sin8x)cos3xcos5xcoz6xcos7x now 15x=7x+8x 7x+8x=Π 8x=Π−7x sin(8x)=sin(Π−7x) sin8x=sin7x 2^4 sinx.k=(2sin7xcos7x)cos3xcos5xcos6x 2^4 sinx.k=sin14x.cos(3×(Π/(15)))(cos5×(Π/(15)))cos(6×(Π/(15)) 15x=14x+x Π=14x+x 14x=Π−x sin(14x)=sin(Π−x)=sinx 2^4 .k=cos36^o ×cos60^o ×cos72^o 2^4 k=cos36^o ×(1/2)×sin18^o 2^5 k=sin18^o ×cos36^o 2^5 k=(((√5) −1)/4)×(((√5) +1)/4) 2^5 k=(4/(16)) 2^5 ×2^2 ×k=1 k=(1/2^7 )
$${cosx}.{cos}\mathrm{2}{x}.{cos}\mathrm{3}{x}.{cos}\mathrm{4}{x}.{cos}\mathrm{5}{x}.{cos}\mathrm{6}{x}.{cos}\mathrm{7}{x}={k} \\ $$$${x}=\frac{\Pi}{\mathrm{15}} \\ $$$$\mathrm{2}{sinx}.{k}=\left(\mathrm{2}{sinxcosx}\right).{cos}\mathrm{2}{x}.{coz}\mathrm{3}{x}.{coz}\mathrm{4}{x}.{cos}\mathrm{5}{x} \\ $$$$\:\:\:\:\:\:\:\:{cos}\mathrm{6}{x}.{cos}\mathrm{7}{x} \\ $$$$\mathrm{2}^{\mathrm{2}} {sinx}.{k}=\left(\mathrm{2}{sin}\mathrm{2}{xcos}\mathrm{2}{x}\right){cos}\mathrm{3}{xcos}\mathrm{4}{xcos}\mathrm{5}{xcos}\mathrm{6}{x} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:{cos}\mathrm{7}{x} \\ $$$$\mathrm{2}^{\mathrm{3}} {sinx}.{k}=\left(\mathrm{2}{sin}\mathrm{4}{xcos}\mathrm{4}{x}\right){cos}\mathrm{3}{xcos}\mathrm{5}{xcos}\mathrm{6}{xco}\mathrm{7}{x} \\ $$$$\mathrm{2}^{\mathrm{3}} {sinx}.{k}=\left({sin}\mathrm{8}{x}\right){cos}\mathrm{3}{xcos}\mathrm{5}{xcoz}\mathrm{6}{xcos}\mathrm{7}{x} \\ $$$${now}\:\:\mathrm{15}{x}=\mathrm{7}{x}+\mathrm{8}{x} \\ $$$$\mathrm{7}{x}+\mathrm{8}{x}=\Pi \\ $$$$\mathrm{8}{x}=\Pi−\mathrm{7}{x} \\ $$$${sin}\left(\mathrm{8}{x}\right)={sin}\left(\Pi−\mathrm{7}{x}\right) \\ $$$${sin}\mathrm{8}{x}={sin}\mathrm{7}{x} \\ $$$$\mathrm{2}^{\mathrm{4}} {sinx}.{k}=\left(\mathrm{2}{sin}\mathrm{7}{xcos}\mathrm{7}{x}\right){cos}\mathrm{3}{xcos}\mathrm{5}{xcos}\mathrm{6}{x} \\ $$$$\mathrm{2}^{\mathrm{4}} {sinx}.{k}={sin}\mathrm{14}{x}.{cos}\left(\mathrm{3}×\frac{\Pi}{\mathrm{15}}\right)\left({cos}\mathrm{5}×\frac{\Pi}{\mathrm{15}}\right){cos}\left(\mathrm{6}×\frac{\Pi}{\mathrm{15}}\right. \\ $$$$\mathrm{15}{x}=\mathrm{14}{x}+{x} \\ $$$$\Pi=\mathrm{14}{x}+{x} \\ $$$$\mathrm{14}{x}=\Pi−{x} \\ $$$${sin}\left(\mathrm{14}{x}\right)={sin}\left(\Pi−{x}\right)={sinx} \\ $$$$\mathrm{2}^{\mathrm{4}} .{k}={cos}\mathrm{36}^{{o}} ×{cos}\mathrm{60}^{{o}} ×{cos}\mathrm{72}^{{o}} \\ $$$$\mathrm{2}^{\mathrm{4}} {k}={cos}\mathrm{36}^{{o}} ×\frac{\mathrm{1}}{\mathrm{2}}×{sin}\mathrm{18}^{{o}} \\ $$$$\mathrm{2}^{\mathrm{5}} {k}={sin}\mathrm{18}^{{o}} ×{cos}\mathrm{36}^{{o}} \\ $$$$\mathrm{2}^{\mathrm{5}} {k}=\frac{\sqrt{\mathrm{5}}\:−\mathrm{1}}{\mathrm{4}}×\frac{\sqrt{\mathrm{5}}\:+\mathrm{1}}{\mathrm{4}} \\ $$$$\mathrm{2}^{\mathrm{5}} {k}=\frac{\mathrm{4}}{\mathrm{16}}\: \\ $$$$\mathrm{2}^{\mathrm{5}} ×\mathrm{2}^{\mathrm{2}} ×{k}=\mathrm{1} \\ $$$${k}=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{7}} } \\ $$
Answered by MrW3 last updated on 18/Jun/18
P=cos (π/(15)) cos ((2π)/(15)) cos ((3π)/(15)) cos ((4π)/(15)) cos ((5π)/(15)) cos ((6π)/(15)) cos ((7π)/(15)) 2 sin (π/(15))P=2 sin (π/(15)) cos (π/(15)) cos ((2π)/(15)) cos ((3π)/(15)) cos ((4π)/(15)) cos ((5π)/(15)) cos ((6π)/(15)) cos ((7π)/(15)) 2 sin (π/(15))P=sin ((2π)/(15)) cos ((2π)/(15)) cos ((3π)/(15)) cos ((4π)/(15)) cos ((5π)/(15)) cos ((6π)/(15)) cos ((7π)/(15)) 2^2 sin (π/(15))P=2 sin ((2π)/(15)) cos ((2π)/(15)) cos ((3π)/(15)) cos ((4π)/(15)) cos ((5π)/(15)) cos ((6π)/(15)) cos ((7π)/(15)) 2^2 sin (π/(15))P=sin ((4π)/(15)) cos ((3π)/(15)) cos ((4π)/(15)) cos ((5π)/(15)) cos ((6π)/(15)) cos ((7π)/(15)) 2^3 sin (π/(15))P=2 sin ((4π)/(15)) cos ((3π)/(15)) cos ((4π)/(15)) cos ((5π)/(15)) cos ((6π)/(15)) cos ((7π)/(15)) 2^3 sin (π/(15))P=sin ((8π)/(15)) cos ((3π)/(15)) cos ((5π)/(15)) cos ((6π)/(15)) cos ((7π)/(15)) 2^4 sin (π/(15))P=2 sin ((8π)/(15)) cos ((3π)/(15)) cos ((5π)/(15)) cos ((6π)/(15)) cos ((7π)/(15)) 2^4 sin (π/(15))P=2 sin ((7π)/(15)) cos ((3π)/(15)) cos ((5π)/(15)) cos ((6π)/(15)) cos ((7π)/(15)) 2^4 sin (π/(15))P=sin ((14π)/(15)) cos ((3π)/(15)) cos ((5π)/(15)) cos ((6π)/(15)) 2^4 sin (π/(15))P=sin (π/(15)) cos ((3π)/(15)) cos ((5π)/(15)) cos ((6π)/(15)) 2^4 P=cos ((3π)/(15)) cos ((5π)/(15)) cos ((6π)/(15)) 2^5 sin ((3π)/(15))P=2 sin ((3π)/(15)) cos ((3π)/(15)) cos ((5π)/(15)) cos ((6π)/(15)) 2^5 sin ((3π)/(15))P=sin ((6π)/(15)) cos ((5π)/(15)) cos ((6π)/(15)) 2^6 sin ((3π)/(15))P=2 sin ((6π)/(15)) cos ((5π)/(15)) cos ((6π)/(15)) 2^6 sin ((3π)/(15))P=sin ((12π)/(15)) cos ((5π)/(15)) 2^6 sin ((3π)/(15))P=sin ((3π)/(15)) cos ((5π)/(15)) 2^6 P=cos ((5π)/(15)) 2^6 P=cos (π/3) 2^6 P=(1/2) ⇒P=(1/2^7 )
$${P}=\mathrm{cos}\:\frac{\pi}{\mathrm{15}}\:\mathrm{cos}\:\frac{\mathrm{2}\pi}{\mathrm{15}}\:\mathrm{cos}\:\frac{\mathrm{3}\pi}{\mathrm{15}}\:\mathrm{cos}\:\frac{\mathrm{4}\pi}{\mathrm{15}}\:\mathrm{cos}\:\frac{\mathrm{5}\pi}{\mathrm{15}}\:\mathrm{cos}\:\frac{\mathrm{6}\pi}{\mathrm{15}}\:\mathrm{cos}\:\frac{\mathrm{7}\pi}{\mathrm{15}}\: \\ $$$$\mathrm{2}\:\mathrm{sin}\:\frac{\pi}{\mathrm{15}}{P}=\mathrm{2}\:\mathrm{sin}\:\frac{\pi}{\mathrm{15}}\:\mathrm{cos}\:\frac{\pi}{\mathrm{15}}\:\mathrm{cos}\:\frac{\mathrm{2}\pi}{\mathrm{15}}\:\mathrm{cos}\:\frac{\mathrm{3}\pi}{\mathrm{15}}\:\mathrm{cos}\:\frac{\mathrm{4}\pi}{\mathrm{15}}\:\mathrm{cos}\:\frac{\mathrm{5}\pi}{\mathrm{15}}\:\mathrm{cos}\:\frac{\mathrm{6}\pi}{\mathrm{15}}\:\mathrm{cos}\:\frac{\mathrm{7}\pi}{\mathrm{15}}\: \\ $$$$\mathrm{2}\:\mathrm{sin}\:\frac{\pi}{\mathrm{15}}{P}=\mathrm{sin}\:\frac{\mathrm{2}\pi}{\mathrm{15}}\:\mathrm{cos}\:\frac{\mathrm{2}\pi}{\mathrm{15}}\:\mathrm{cos}\:\frac{\mathrm{3}\pi}{\mathrm{15}}\:\mathrm{cos}\:\frac{\mathrm{4}\pi}{\mathrm{15}}\:\mathrm{cos}\:\frac{\mathrm{5}\pi}{\mathrm{15}}\:\mathrm{cos}\:\frac{\mathrm{6}\pi}{\mathrm{15}}\:\mathrm{cos}\:\frac{\mathrm{7}\pi}{\mathrm{15}}\: \\ $$$$\mathrm{2}^{\mathrm{2}} \:\mathrm{sin}\:\frac{\pi}{\mathrm{15}}{P}=\mathrm{2}\:\mathrm{sin}\:\frac{\mathrm{2}\pi}{\mathrm{15}}\:\mathrm{cos}\:\frac{\mathrm{2}\pi}{\mathrm{15}}\:\mathrm{cos}\:\frac{\mathrm{3}\pi}{\mathrm{15}}\:\mathrm{cos}\:\frac{\mathrm{4}\pi}{\mathrm{15}}\:\mathrm{cos}\:\frac{\mathrm{5}\pi}{\mathrm{15}}\:\mathrm{cos}\:\frac{\mathrm{6}\pi}{\mathrm{15}}\:\mathrm{cos}\:\frac{\mathrm{7}\pi}{\mathrm{15}}\: \\ $$$$\mathrm{2}^{\mathrm{2}} \:\mathrm{sin}\:\frac{\pi}{\mathrm{15}}{P}=\mathrm{sin}\:\frac{\mathrm{4}\pi}{\mathrm{15}}\:\mathrm{cos}\:\frac{\mathrm{3}\pi}{\mathrm{15}}\:\mathrm{cos}\:\frac{\mathrm{4}\pi}{\mathrm{15}}\:\mathrm{cos}\:\frac{\mathrm{5}\pi}{\mathrm{15}}\:\mathrm{cos}\:\frac{\mathrm{6}\pi}{\mathrm{15}}\:\mathrm{cos}\:\frac{\mathrm{7}\pi}{\mathrm{15}}\: \\ $$$$\mathrm{2}^{\mathrm{3}} \:\mathrm{sin}\:\frac{\pi}{\mathrm{15}}{P}=\mathrm{2}\:\mathrm{sin}\:\frac{\mathrm{4}\pi}{\mathrm{15}}\:\mathrm{cos}\:\frac{\mathrm{3}\pi}{\mathrm{15}}\:\mathrm{cos}\:\frac{\mathrm{4}\pi}{\mathrm{15}}\:\mathrm{cos}\:\frac{\mathrm{5}\pi}{\mathrm{15}}\:\mathrm{cos}\:\frac{\mathrm{6}\pi}{\mathrm{15}}\:\mathrm{cos}\:\frac{\mathrm{7}\pi}{\mathrm{15}}\: \\ $$$$\mathrm{2}^{\mathrm{3}} \:\mathrm{sin}\:\frac{\pi}{\mathrm{15}}{P}=\mathrm{sin}\:\frac{\mathrm{8}\pi}{\mathrm{15}}\:\mathrm{cos}\:\frac{\mathrm{3}\pi}{\mathrm{15}}\:\mathrm{cos}\:\frac{\mathrm{5}\pi}{\mathrm{15}}\:\mathrm{cos}\:\frac{\mathrm{6}\pi}{\mathrm{15}}\:\mathrm{cos}\:\frac{\mathrm{7}\pi}{\mathrm{15}}\: \\ $$$$\mathrm{2}^{\mathrm{4}} \:\mathrm{sin}\:\frac{\pi}{\mathrm{15}}{P}=\mathrm{2}\:\mathrm{sin}\:\frac{\mathrm{8}\pi}{\mathrm{15}}\:\mathrm{cos}\:\frac{\mathrm{3}\pi}{\mathrm{15}}\:\mathrm{cos}\:\frac{\mathrm{5}\pi}{\mathrm{15}}\:\mathrm{cos}\:\frac{\mathrm{6}\pi}{\mathrm{15}}\:\mathrm{cos}\:\frac{\mathrm{7}\pi}{\mathrm{15}}\: \\ $$$$\mathrm{2}^{\mathrm{4}} \:\mathrm{sin}\:\frac{\pi}{\mathrm{15}}{P}=\mathrm{2}\:\mathrm{sin}\:\frac{\mathrm{7}\pi}{\mathrm{15}}\:\mathrm{cos}\:\frac{\mathrm{3}\pi}{\mathrm{15}}\:\mathrm{cos}\:\frac{\mathrm{5}\pi}{\mathrm{15}}\:\mathrm{cos}\:\frac{\mathrm{6}\pi}{\mathrm{15}}\:\mathrm{cos}\:\frac{\mathrm{7}\pi}{\mathrm{15}}\: \\ $$$$\mathrm{2}^{\mathrm{4}} \:\mathrm{sin}\:\frac{\pi}{\mathrm{15}}{P}=\mathrm{sin}\:\frac{\mathrm{14}\pi}{\mathrm{15}}\:\mathrm{cos}\:\frac{\mathrm{3}\pi}{\mathrm{15}}\:\mathrm{cos}\:\frac{\mathrm{5}\pi}{\mathrm{15}}\:\mathrm{cos}\:\frac{\mathrm{6}\pi}{\mathrm{15}} \\ $$$$\mathrm{2}^{\mathrm{4}} \:\mathrm{sin}\:\frac{\pi}{\mathrm{15}}{P}=\mathrm{sin}\:\frac{\pi}{\mathrm{15}}\:\mathrm{cos}\:\frac{\mathrm{3}\pi}{\mathrm{15}}\:\mathrm{cos}\:\frac{\mathrm{5}\pi}{\mathrm{15}}\:\mathrm{cos}\:\frac{\mathrm{6}\pi}{\mathrm{15}} \\ $$$$\mathrm{2}^{\mathrm{4}} \:{P}=\mathrm{cos}\:\frac{\mathrm{3}\pi}{\mathrm{15}}\:\mathrm{cos}\:\frac{\mathrm{5}\pi}{\mathrm{15}}\:\mathrm{cos}\:\frac{\mathrm{6}\pi}{\mathrm{15}} \\ $$$$\mathrm{2}^{\mathrm{5}} \:\mathrm{sin}\:\frac{\mathrm{3}\pi}{\mathrm{15}}{P}=\mathrm{2}\:\mathrm{sin}\:\frac{\mathrm{3}\pi}{\mathrm{15}}\:\mathrm{cos}\:\frac{\mathrm{3}\pi}{\mathrm{15}}\:\mathrm{cos}\:\frac{\mathrm{5}\pi}{\mathrm{15}}\:\mathrm{cos}\:\frac{\mathrm{6}\pi}{\mathrm{15}} \\ $$$$\mathrm{2}^{\mathrm{5}} \:\mathrm{sin}\:\frac{\mathrm{3}\pi}{\mathrm{15}}{P}=\mathrm{sin}\:\frac{\mathrm{6}\pi}{\mathrm{15}}\:\mathrm{cos}\:\frac{\mathrm{5}\pi}{\mathrm{15}}\:\mathrm{cos}\:\frac{\mathrm{6}\pi}{\mathrm{15}} \\ $$$$\mathrm{2}^{\mathrm{6}} \:\mathrm{sin}\:\frac{\mathrm{3}\pi}{\mathrm{15}}{P}=\mathrm{2}\:\mathrm{sin}\:\frac{\mathrm{6}\pi}{\mathrm{15}}\:\mathrm{cos}\:\frac{\mathrm{5}\pi}{\mathrm{15}}\:\mathrm{cos}\:\frac{\mathrm{6}\pi}{\mathrm{15}} \\ $$$$\mathrm{2}^{\mathrm{6}} \:\mathrm{sin}\:\frac{\mathrm{3}\pi}{\mathrm{15}}{P}=\mathrm{sin}\:\frac{\mathrm{12}\pi}{\mathrm{15}}\:\mathrm{cos}\:\frac{\mathrm{5}\pi}{\mathrm{15}} \\ $$$$\mathrm{2}^{\mathrm{6}} \:\mathrm{sin}\:\frac{\mathrm{3}\pi}{\mathrm{15}}{P}=\mathrm{sin}\:\frac{\mathrm{3}\pi}{\mathrm{15}}\:\mathrm{cos}\:\frac{\mathrm{5}\pi}{\mathrm{15}} \\ $$$$\mathrm{2}^{\mathrm{6}} \:{P}=\mathrm{cos}\:\frac{\mathrm{5}\pi}{\mathrm{15}} \\ $$$$\mathrm{2}^{\mathrm{6}} \:{P}=\mathrm{cos}\:\frac{\pi}{\mathrm{3}} \\ $$$$\mathrm{2}^{\mathrm{6}} \:{P}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow{P}=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{7}} } \\ $$
Commented by kunal1234523 last updated on 18/Jun/18
I appreciate your hard work
$$\mathrm{I}\:\mathrm{appreciate}\:\mathrm{your}\:\mathrm{hard}\:\mathrm{work} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *