Menu Close

prove-that-cos-x-2-2x-x-2-2-dx-pi-e-cos-1-

Tinku Tara 0 Comments
Pin




Question Number 162073 by mnjuly1970 last updated on 26/Dec/21
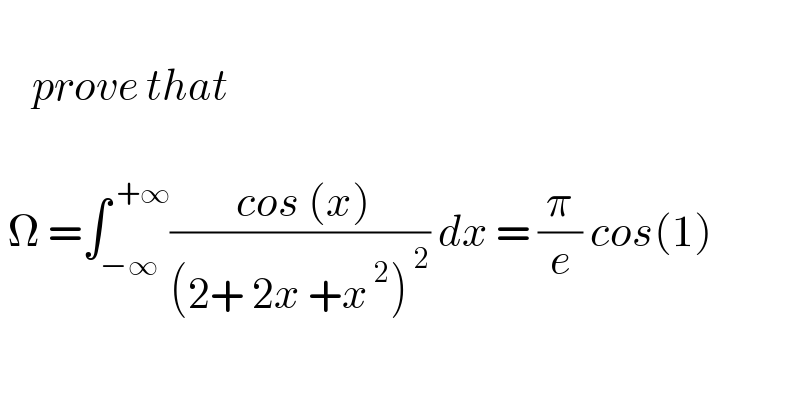
prove that Ω =∫_(−∞) ^( +∞) (( cos (x))/((2+ 2x +x^( 2) )^( 2) )) dx = (π/e) cos(1)
$$ \\ $$$$\:\:\:\:{prove}\:{that} \\ $$$$ \\ $$$$\:\Omega\:=\int_{−\infty} ^{\:+\infty} \frac{\:{cos}\:\left({x}\right)}{\left(\mathrm{2}+\:\mathrm{2}{x}\:+{x}^{\:\mathrm{2}} \right)^{\:\mathrm{2}} }\:{dx}\:=\:\frac{\pi}{{e}}\:{cos}\left(\mathrm{1}\right) \\ $$
Answered by mindispower last updated on 26/Dec/21
Ω=∫_(−∞) ^∞ ((cos(x))/((1+(1+x)^2 )^2 ))dx 1+x=t =∫_(−∞) ^∞ ((cos(t−1))/((1+t^2 )^2 ))dt=∫_(−∞) ^∞ ((cos(t)cos(1))/((1+t^2 )^2 ))dt+sin(1)∫_(−∞) ^∞ ((sin(t))/((1+t^2 )^2 ))dt_(=0) =cos(1)∫_(−∞) ^∞ ((cos(t)dt)/((1+t^2 )^2 )) f(a)=∫_(−∞) ^∞ ((cos(t))/(a^2 +t^2 ))=Re∫_(−∞) ^∞ (e^(it) /(a^2 +t^2 ))=Re(2iπ.e^(−a) .(1/(2ia))) =(π/a)e^(−a) =f(a) f′(a)=∫_(−∞) ^∞ ((−2acos(t))/((a^2 +t^2 )^2 ))dt f′(1)=−2∫_(−∞) ^∞ ((cos(t)dt)/((1+t^2 )^2 )) f′(a)=(−(π/a^2 )e^(−a) −(π/a)e^(−a) ) ∫_(−∞) ^∞ ((cos(t)dt)/((1+t^2 )^2 ))=(1/2).((2π)/e)=(π/e) ∫_(−∞) ^∞ ((cost))/((2+2t+t^2 )^2 ))dt=cos(1)∫((cos(x))/((1+x^2 )^2 ))dx=cos(1)(π/e)
$$\Omega=\int_{−\infty} ^{\infty} \frac{{cos}\left({x}\right)}{\left(\mathrm{1}+\left(\mathrm{1}+{x}\right)^{\mathrm{2}} \right)^{\mathrm{2}} }{dx} \\ $$$$\mathrm{1}+{x}={t} \\ $$$$=\int_{−\infty} ^{\infty} \frac{{cos}\left({t}−\mathrm{1}\right)}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} }{dt}=\int_{−\infty} ^{\infty} \frac{{cos}\left({t}\right){cos}\left(\mathrm{1}\right)}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} }{dt}+{sin}\left(\mathrm{1}\right)\int_{−\infty} ^{\infty} \frac{{sin}\left({t}\right)}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} }{dt}_{=\mathrm{0}} \\ $$$$={cos}\left(\mathrm{1}\right)\int_{−\infty} ^{\infty} \frac{{cos}\left({t}\right){dt}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$${f}\left({a}\right)=\int_{−\infty} ^{\infty} \frac{{cos}\left({t}\right)}{{a}^{\mathrm{2}} +{t}^{\mathrm{2}} }={Re}\int_{−\infty} ^{\infty} \frac{{e}^{{it}} }{{a}^{\mathrm{2}} +{t}^{\mathrm{2}} }={Re}\left(\mathrm{2}{i}\pi.{e}^{−{a}} .\frac{\mathrm{1}}{\mathrm{2}{ia}}\right) \\ $$$$=\frac{\pi}{{a}}{e}^{−{a}} ={f}\left({a}\right) \\ $$$${f}'\left({a}\right)=\int_{−\infty} ^{\infty} \frac{−\mathrm{2}{acos}\left({t}\right)}{\left({a}^{\mathrm{2}} +{t}^{\mathrm{2}} \right)^{\mathrm{2}} }{dt} \\ $$$${f}'\left(\mathrm{1}\right)=−\mathrm{2}\int_{−\infty} ^{\infty} \frac{{cos}\left({t}\right){dt}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$${f}'\left({a}\right)=\left(−\frac{\pi}{{a}^{\mathrm{2}} }{e}^{−{a}} −\frac{\pi}{{a}}{e}^{−{a}} \right) \\ $$$$\int_{−\infty} ^{\infty} \frac{{cos}\left({t}\right){dt}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{2}}.\frac{\mathrm{2}\pi}{{e}}=\frac{\pi}{{e}} \\ $$$$\int_{−\infty} ^{\infty} \frac{\left.{cost}\right)}{\left(\mathrm{2}+\mathrm{2}{t}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} }{dt}={cos}\left(\mathrm{1}\right)\int\frac{{cos}\left({x}\right)}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} }{dx}={cos}\left(\mathrm{1}\right)\frac{\pi}{{e}} \\ $$$$ \\ $$
Commented by Tawa11 last updated on 26/Dec/21
Great sir
$$\mathrm{Great}\:\mathrm{sir} \\ $$
Commented by mnjuly1970 last updated on 26/Dec/21
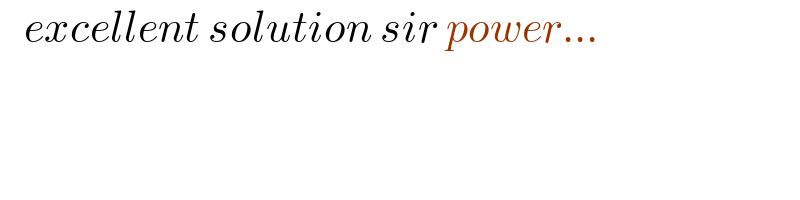
excellent solution sir power...
$$\:\:\:{excellent}\:{solution}\:{sir}\:{power}… \\ $$
Answered by Mathspace last updated on 26/Dec/21
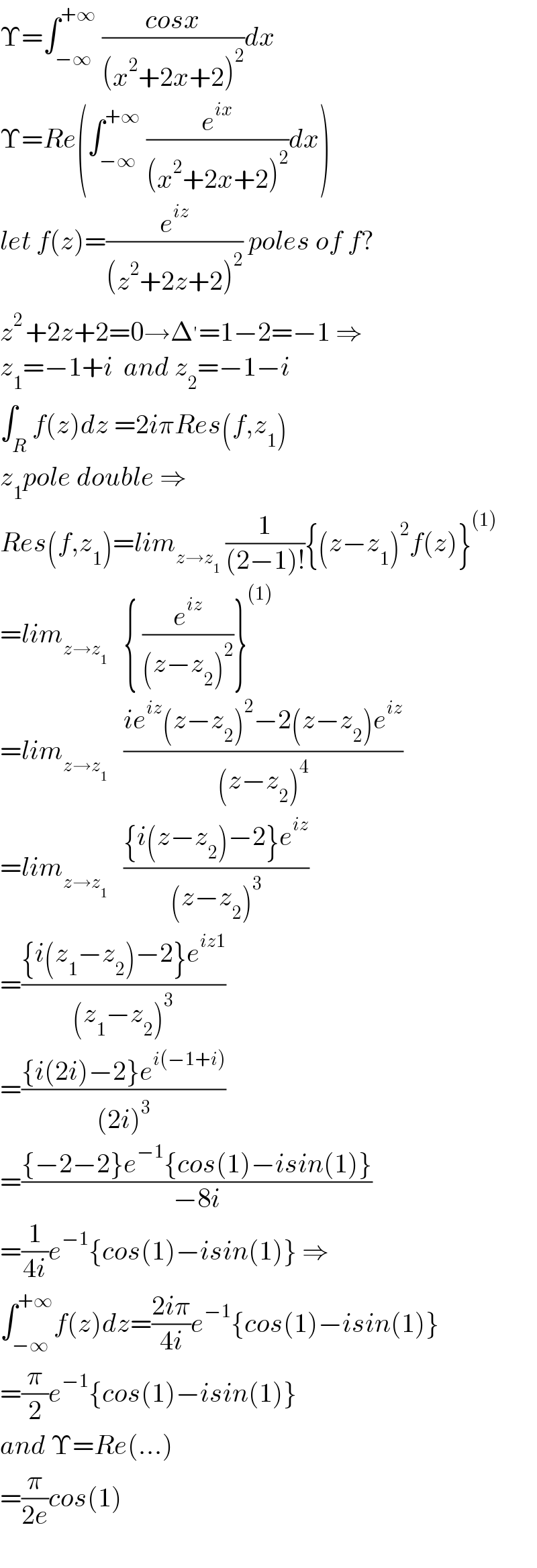
Υ=∫_(−∞) ^(+∞) ((cosx)/((x^2 +2x+2)^2 ))dx Υ=Re(∫_(−∞) ^(+∞) (e^(ix) /((x^2 +2x+2)^2 ))dx) let f(z)=(e^(iz) /((z^2 +2z+2)^2 )) poles of f? z^(2 ) +2z+2=0→Δ^′ =1−2=−1 ⇒ z_1 =−1+i and z_2 =−1−i ∫_R f(z)dz =2iπRes(f,z_1 ) z_1 pole double ⇒ Res(f,z_1 )=lim_(z→z_1 ) (1/((2−1)!)){(z−z_1 )^2 f(z)}^((1)) =lim_(z→z_1 ) { (e^(iz) /((z−z_2 )^2 ))}^((1)) =lim_(z→z_1 ) ((ie^(iz) (z−z_2 )^2 −2(z−z_2 )e^(iz) )/((z−z_2 )^4 )) =lim_(z→z_1 ) (({i(z−z_2 )−2}e^(iz) )/((z−z_2 )^3 )) =(({i(z_1 −z_2 )−2}e^(iz1) )/((z_1 −z_2 )^3 )) =(({i(2i)−2}e^(i(−1+i)) )/((2i)^3 )) =(({−2−2}e^(−1) {cos(1)−isin(1)})/(−8i)) =(1/(4i))e^(−1) {cos(1)−isin(1)} ⇒ ∫_(−∞) ^(+∞) f(z)dz=((2iπ)/(4i))e^(−1) {cos(1)−isin(1)} =(π/2)e^(−1) {cos(1)−isin(1)} and Υ=Re(...) =(π/(2e))cos(1)
$$\Upsilon=\int_{−\infty} ^{+\infty} \:\frac{{cosx}}{\left({x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{2}\right)^{\mathrm{2}} }{dx} \\ $$$$\Upsilon={Re}\left(\int_{−\infty} ^{+\infty} \:\frac{{e}^{{ix}} }{\left({x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{2}\right)^{\mathrm{2}} }{dx}\right) \\ $$$${let}\:{f}\left({z}\right)=\frac{{e}^{{iz}} }{\left({z}^{\mathrm{2}} +\mathrm{2}{z}+\mathrm{2}\right)^{\mathrm{2}} }\:{poles}\:{of}\:{f}? \\ $$$${z}^{\mathrm{2}\:} +\mathrm{2}{z}+\mathrm{2}=\mathrm{0}\rightarrow\Delta^{'} =\mathrm{1}−\mathrm{2}=−\mathrm{1}\:\Rightarrow \\ $$$${z}_{\mathrm{1}} =−\mathrm{1}+{i}\:\:{and}\:{z}_{\mathrm{2}} =−\mathrm{1}−{i} \\ $$$$\int_{{R}} {f}\left({z}\right){dz}\:=\mathrm{2}{i}\pi{Res}\left({f},{z}_{\mathrm{1}} \right) \\ $$$${z}_{\mathrm{1}} {pole}\:{double}\:\Rightarrow \\ $$$${Res}\left({f},{z}_{\mathrm{1}} \right)={lim}_{{z}\rightarrow{z}_{\mathrm{1}} } \:\frac{\mathrm{1}}{\left(\mathrm{2}−\mathrm{1}\right)!}\left\{\left({z}−{z}_{\mathrm{1}} \right)^{\mathrm{2}} {f}\left({z}\right)\right\}^{\left(\mathrm{1}\right)} \\ $$$$={lim}_{{z}\rightarrow{z}_{\mathrm{1}} } \:\:\:\left\{\:\frac{{e}^{{iz}} }{\left({z}−{z}_{\mathrm{2}} \right)^{\mathrm{2}} }\right\}^{\left(\mathrm{1}\right)} \\ $$$$={lim}_{{z}\rightarrow{z}_{\mathrm{1}} } \:\:\:\frac{{ie}^{{iz}} \left({z}−{z}_{\mathrm{2}} \right)^{\mathrm{2}} −\mathrm{2}\left({z}−{z}_{\mathrm{2}} \right){e}^{{iz}} }{\left({z}−{z}_{\mathrm{2}} \right)^{\mathrm{4}} } \\ $$$$={lim}_{{z}\rightarrow{z}_{\mathrm{1}} } \:\:\:\frac{\left\{{i}\left({z}−{z}_{\mathrm{2}} \right)−\mathrm{2}\right\}{e}^{{iz}} }{\left({z}−{z}_{\mathrm{2}} \right)^{\mathrm{3}} } \\ $$$$=\frac{\left\{{i}\left({z}_{\mathrm{1}} −{z}_{\mathrm{2}} \right)−\mathrm{2}\right\}{e}^{{iz}\mathrm{1}} }{\left({z}_{\mathrm{1}} −{z}_{\mathrm{2}} \right)^{\mathrm{3}} } \\ $$$$=\frac{\left\{{i}\left(\mathrm{2}{i}\right)−\mathrm{2}\right\}{e}^{{i}\left(−\mathrm{1}+{i}\right)} }{\left(\mathrm{2}{i}\right)^{\mathrm{3}} } \\ $$$$=\frac{\left\{−\mathrm{2}−\mathrm{2}\right\}{e}^{−\mathrm{1}} \left\{{cos}\left(\mathrm{1}\right)−{isin}\left(\mathrm{1}\right)\right\}}{−\mathrm{8}{i}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}{i}}{e}^{−\mathrm{1}} \left\{{cos}\left(\mathrm{1}\right)−{isin}\left(\mathrm{1}\right)\right\}\:\Rightarrow \\ $$$$\int_{−\infty} ^{+\infty} {f}\left({z}\right){dz}=\frac{\mathrm{2}{i}\pi}{\mathrm{4}{i}}{e}^{−\mathrm{1}} \left\{{cos}\left(\mathrm{1}\right)−{isin}\left(\mathrm{1}\right)\right\} \\ $$$$=\frac{\pi}{\mathrm{2}}{e}^{−\mathrm{1}} \left\{{cos}\left(\mathrm{1}\right)−{isin}\left(\mathrm{1}\right)\right\} \\ $$$${and}\:\Upsilon={Re}\left(…\right) \\ $$$$=\frac{\pi}{\mathrm{2}{e}}{cos}\left(\mathrm{1}\right) \\ $$$$ \\ $$
Commented by mnjuly1970 last updated on 26/Dec/21
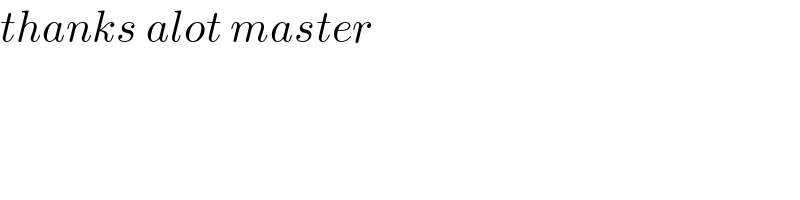
thanks alot master
$${thanks}\:{alot}\:{master} \\ $$
Answered by Ar Brandon last updated on 24/Mar/22
Ω=∫_(−∞) ^(+∞) ((cosx)/((x^2 +2x+2)^2 ))dx ϕ(z)=(e^(iz) /((z^2 +2z+2)^2 )) , Poles: z_1 =((−2+2i)/2)=(√2)e^(((3π)/4)i) , z_2 =(√2)e^(−(π/4)i) Ω=Re∫_(−∞) ^(+∞) ϕ(z)dz=Re(2iπRes(ϕ, z_1 )) Res (ϕ, z_1 )=lim_(z→z_1 ) (d/dz){(z−z_1 )^2 ϕ(z)}=lim_(z→z_1 ) (d/dz){(e^(iz) /((z−z_2 )^2 ))} =lim_(z→z_1 ) {((ie^(iz) (z−z_2 )^2 −2e^(iz) (z−z_2 ))/((z−z_2 )^4 ))}=((ie^(iz_1 ) (z_1 −z_2 )^2 −2e^(iz_1 ) (z_1 −z_2 ))/((z_1 −z_2 )^4 )) =((ie^(i(−1+i)) (2i)^2 −2e^(i(−1+i)) (2i))/(16))=−((4ie^(−(1+i)) +4ie^(−(1+i)) )/(16)) =−(1/(2e))×e^(((π/2)−1)i) =−(1/(2e))(sin(1)+icos(1)) ⇒Re(2iπRes(ϕ, z_1 )=(π/e)cos(1) ⇒ determinant (((∫_(−∞) ^(+∞) ((cosx)/((x^2 +2x+2)^2 ))dx=(π/e)cos(1))))
$$\Omega=\int_{−\infty} ^{+\infty} \frac{\mathrm{cos}{x}}{\left({x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{2}\right)^{\mathrm{2}} }{dx} \\ $$$$\varphi\left({z}\right)=\frac{{e}^{{iz}} }{\left({z}^{\mathrm{2}} +\mathrm{2}{z}+\mathrm{2}\right)^{\mathrm{2}} }\:\:\:\:,\:\:\:\mathrm{Poles}:\:{z}_{\mathrm{1}} =\frac{−\mathrm{2}+\mathrm{2}{i}}{\mathrm{2}}=\sqrt{\mathrm{2}}{e}^{\frac{\mathrm{3}\pi}{\mathrm{4}}{i}} ,\:{z}_{\mathrm{2}} =\sqrt{\mathrm{2}}{e}^{−\frac{\pi}{\mathrm{4}}{i}} \\ $$$$\Omega={Re}\int_{−\infty} ^{+\infty} \varphi\left({z}\right){dz}={Re}\left(\mathrm{2i}\pi{Res}\left(\varphi,\:{z}_{\mathrm{1}} \right)\right) \\ $$$${Res}\:\left(\varphi,\:{z}_{\mathrm{1}} \right)=\underset{{z}\rightarrow{z}_{\mathrm{1}} } {\mathrm{lim}}\frac{\mathrm{d}}{\mathrm{d}{z}}\left\{\left({z}−{z}_{\mathrm{1}} \right)^{\mathrm{2}} \varphi\left({z}\right)\right\}=\underset{{z}\rightarrow{z}_{\mathrm{1}} } {\mathrm{lim}}\frac{\mathrm{d}}{\mathrm{d}{z}}\left\{\frac{{e}^{{iz}} }{\left({z}−{z}_{\mathrm{2}} \right)^{\mathrm{2}} }\right\} \\ $$$$=\underset{{z}\rightarrow{z}_{\mathrm{1}} } {\mathrm{lim}}\left\{\frac{{ie}^{{iz}} \left({z}−{z}_{\mathrm{2}} \right)^{\mathrm{2}} −\mathrm{2}{e}^{{iz}} \left({z}−{z}_{\mathrm{2}} \right)}{\left({z}−{z}_{\mathrm{2}} \right)^{\mathrm{4}} }\right\}=\frac{{ie}^{{iz}_{\mathrm{1}} } \left({z}_{\mathrm{1}} −{z}_{\mathrm{2}} \right)^{\mathrm{2}} −\mathrm{2}{e}^{{iz}_{\mathrm{1}} } \left({z}_{\mathrm{1}} −{z}_{\mathrm{2}} \right)}{\left({z}_{\mathrm{1}} −{z}_{\mathrm{2}} \right)^{\mathrm{4}} } \\ $$$$=\frac{{ie}^{{i}\left(−\mathrm{1}+{i}\right)} \left(\mathrm{2}{i}\right)^{\mathrm{2}} −\mathrm{2}{e}^{{i}\left(−\mathrm{1}+{i}\right)} \left(\mathrm{2}{i}\right)}{\mathrm{16}}=−\frac{\mathrm{4}{ie}^{−\left(\mathrm{1}+{i}\right)} +\mathrm{4}{ie}^{−\left(\mathrm{1}+{i}\right)} }{\mathrm{16}} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}{e}}×{e}^{\left(\frac{\pi}{\mathrm{2}}−\mathrm{1}\right){i}} =−\frac{\mathrm{1}}{\mathrm{2}{e}}\left(\mathrm{sin}\left(\mathrm{1}\right)+{i}\mathrm{cos}\left(\mathrm{1}\right)\right) \\ $$$$\Rightarrow{Re}\left(\mathrm{2}{i}\pi{Res}\left(\varphi,\:{z}_{\mathrm{1}} \right)=\frac{\pi}{{e}}\mathrm{cos}\left(\mathrm{1}\right)\right. \\ $$$$\Rightarrow\begin{array}{|c|}{\int_{−\infty} ^{+\infty} \frac{\mathrm{cos}{x}}{\left({x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{2}\right)^{\mathrm{2}} }{dx}=\frac{\pi}{{e}}\mathrm{cos}\left(\mathrm{1}\right)}\\\hline\end{array} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *