Question Number 13626 by tawa tawa last updated on 21/May/17
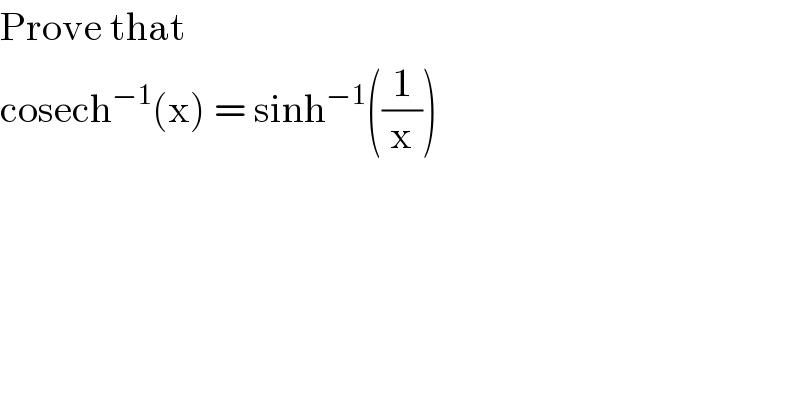
$$\mathrm{Prove}\:\mathrm{that} \\ $$$$\mathrm{cosech}^{−\mathrm{1}} \left(\mathrm{x}\right)\:=\:\mathrm{sinh}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{x}}\right) \\ $$
Answered by mrW1 last updated on 21/May/17
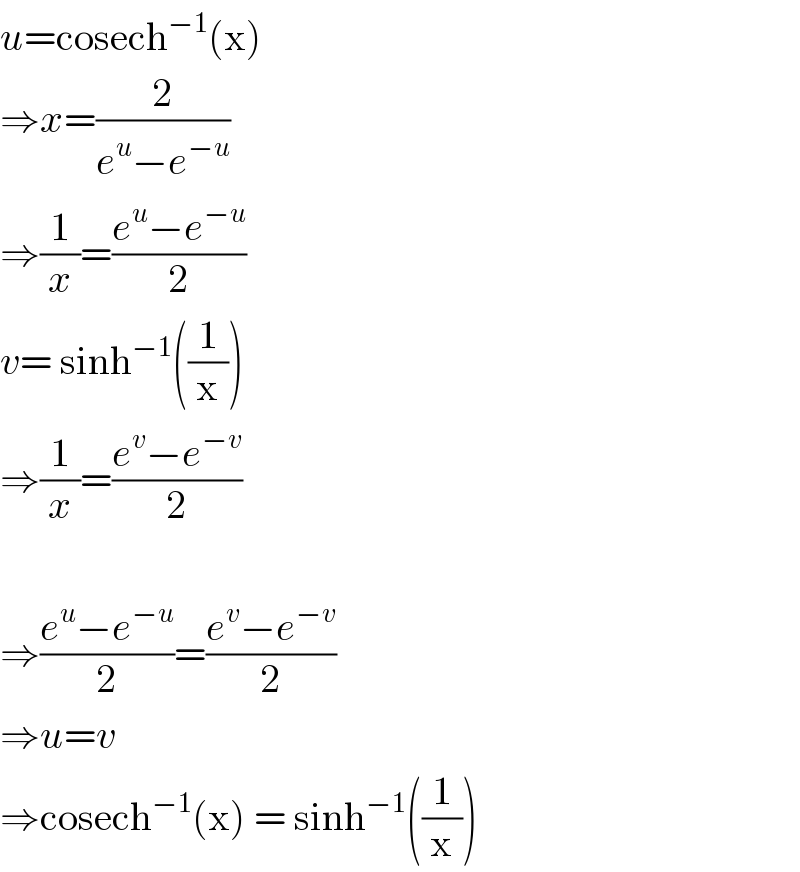
$${u}=\mathrm{cosech}^{−\mathrm{1}} \left(\mathrm{x}\right)\: \\ $$$$\Rightarrow{x}=\frac{\mathrm{2}}{{e}^{{u}} −{e}^{−{u}} } \\ $$$$\Rightarrow\frac{\mathrm{1}}{{x}}=\frac{{e}^{{u}} −{e}^{−{u}} }{\mathrm{2}} \\ $$$${v}=\:\mathrm{sinh}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{x}}\right) \\ $$$$\Rightarrow\frac{\mathrm{1}}{{x}}=\frac{{e}^{{v}} −{e}^{−{v}} }{\mathrm{2}} \\ $$$$ \\ $$$$\Rightarrow\frac{{e}^{{u}} −{e}^{−{u}} }{\mathrm{2}}=\frac{{e}^{{v}} −{e}^{−{v}} }{\mathrm{2}} \\ $$$$\Rightarrow{u}={v} \\ $$$$\Rightarrow\mathrm{cosech}^{−\mathrm{1}} \left(\mathrm{x}\right)\:=\:\mathrm{sinh}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{x}}\right) \\ $$
Commented by tawa tawa last updated on 21/May/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
