Question Number 17280 by tawa tawa last updated on 03/Jul/17
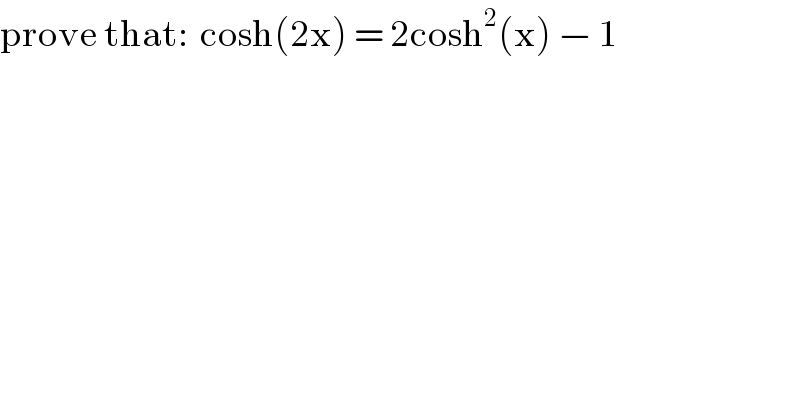
$$\mathrm{prove}\:\mathrm{that}:\:\:\mathrm{cosh}\left(\mathrm{2x}\right)\:=\:\mathrm{2cosh}^{\mathrm{2}} \left(\mathrm{x}\right)\:−\:\mathrm{1} \\ $$
Commented by mrW1 last updated on 03/Jul/17
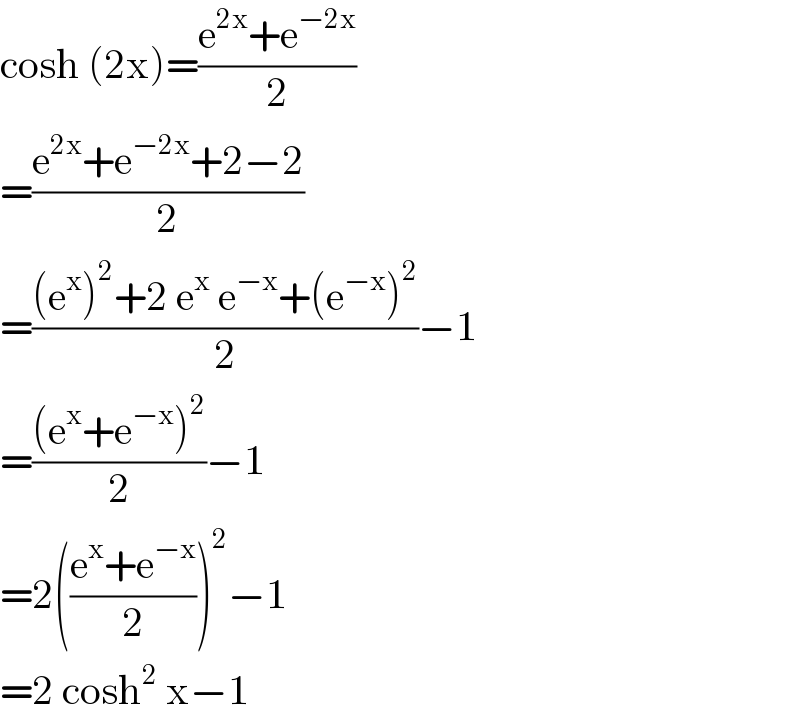
$$\mathrm{cosh}\:\left(\mathrm{2x}\right)=\frac{\mathrm{e}^{\mathrm{2x}} +\mathrm{e}^{−\mathrm{2x}} }{\mathrm{2}} \\ $$$$=\frac{\mathrm{e}^{\mathrm{2x}} +\mathrm{e}^{−\mathrm{2x}} +\mathrm{2}−\mathrm{2}}{\mathrm{2}} \\ $$$$=\frac{\left(\mathrm{e}^{\mathrm{x}} \right)^{\mathrm{2}} +\mathrm{2}\:\mathrm{e}^{\mathrm{x}} \:\mathrm{e}^{−\mathrm{x}} +\left(\mathrm{e}^{−\mathrm{x}} \right)^{\mathrm{2}} }{\mathrm{2}}−\mathrm{1} \\ $$$$=\frac{\left(\mathrm{e}^{\mathrm{x}} +\mathrm{e}^{−\mathrm{x}} \right)^{\mathrm{2}} }{\mathrm{2}}−\mathrm{1} \\ $$$$=\mathrm{2}\left(\frac{\mathrm{e}^{\mathrm{x}} +\mathrm{e}^{−\mathrm{x}} }{\mathrm{2}}\right)^{\mathrm{2}} −\mathrm{1} \\ $$$$=\mathrm{2}\:\mathrm{cosh}^{\mathrm{2}} \:\mathrm{x}−\mathrm{1} \\ $$
Commented by tawa tawa last updated on 03/Jul/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\: \\ $$
