Menu Close

prove-that-cot5x-1-10tan-2-x-5tan-4-x-tan-5-x-10tan-3-x-5tanx-

Tinku Tara 0 Comments
Pin




Question Number 123232 by mohammad17 last updated on 24/Nov/20
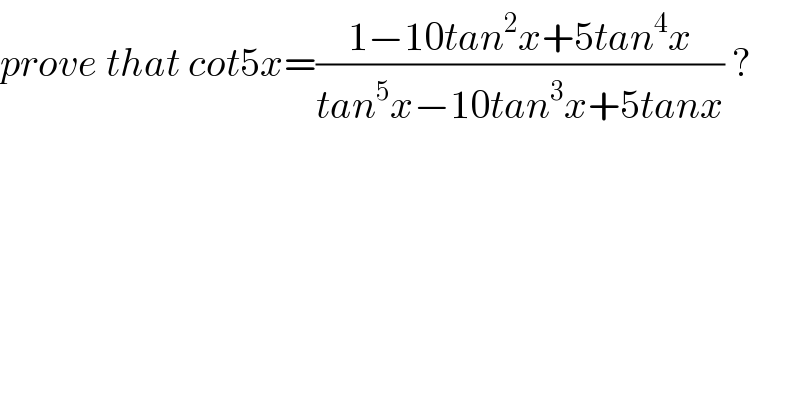
prove that cot5x=((1−10tan^2 x+5tan^4 x)/(tan^5 x−10tan^3 x+5tanx)) ?
$${prove}\:{that}\:{cot}\mathrm{5}{x}=\frac{\mathrm{1}−\mathrm{10}{tan}^{\mathrm{2}} {x}+\mathrm{5}{tan}^{\mathrm{4}} {x}}{{tan}^{\mathrm{5}} {x}−\mathrm{10}{tan}^{\mathrm{3}} {x}+\mathrm{5}{tanx}}\:? \\ $$
Answered by $@y@m last updated on 24/Nov/20
tan (2x+3x)=((tan 2x+tan 3x)/(1−tan 2x.tan 3x)) ⇒ tan5x=((((2tan x)/(1−tan^2 x))+((3tan x−tan^3 x)/(1−3tan^2 x)))/(1−(((2tan x)/(1−tan^2 x)))(((3tan x−tan^3 x)/(1−3tan^2 x))))) =((2tan x(1−3tan^2 x)+(1−tan^2 x)(3tan x−tan^3 x))/((1−tan^2 x)(1−3tan^2 x)−2tan x(3tan x−tan^3 x))) =((2tan x−6tan^3 x+3tan x−3tan^3 x−tan^3 x+tan^5 x)/(1−tan^2 x−3tan^2 x+3tan^4 x−6tan^2 x+2tan^4 x)) =((tan^5 x−10tan^3 x+5tan x)/(1−10tan^2 x+5tan^4 x))
$$\mathrm{tan}\:\left(\mathrm{2}{x}+\mathrm{3}{x}\right)=\frac{\mathrm{tan}\:\mathrm{2}{x}+\mathrm{tan}\:\mathrm{3}{x}}{\mathrm{1}−\mathrm{tan}\:\mathrm{2}{x}.\mathrm{tan}\:\mathrm{3}{x}} \\ $$$$\Rightarrow\:\mathrm{tan5}{x}=\frac{\frac{\mathrm{2tan}\:{x}}{\mathrm{1}−\mathrm{tan}\:^{\mathrm{2}} {x}}+\frac{\mathrm{3tan}\:{x}−\mathrm{tan}\:^{\mathrm{3}} {x}}{\mathrm{1}−\mathrm{3tan}\:^{\mathrm{2}} {x}}}{\mathrm{1}−\left(\frac{\mathrm{2tan}\:{x}}{\mathrm{1}−\mathrm{tan}\:^{\mathrm{2}} {x}}\right)\left(\frac{\mathrm{3tan}\:{x}−\mathrm{tan}\:^{\mathrm{3}} {x}}{\mathrm{1}−\mathrm{3tan}\:^{\mathrm{2}} {x}}\right)} \\ $$$$=\frac{\mathrm{2tan}\:{x}\left(\mathrm{1}−\mathrm{3tan}\:^{\mathrm{2}} {x}\right)+\left(\mathrm{1}−\mathrm{tan}\:^{\mathrm{2}} {x}\right)\left(\mathrm{3tan}\:{x}−\mathrm{tan}\:^{\mathrm{3}} {x}\right)}{\left(\mathrm{1}−\mathrm{tan}\:^{\mathrm{2}} {x}\right)\left(\mathrm{1}−\mathrm{3tan}\:^{\mathrm{2}} {x}\right)−\mathrm{2tan}\:{x}\left(\mathrm{3tan}\:{x}−\mathrm{tan}\:^{\mathrm{3}} {x}\right)} \\ $$$$=\frac{\mathrm{2tan}\:{x}−\mathrm{6tan}^{\mathrm{3}} {x}+\mathrm{3tan}\:{x}−\mathrm{3tan}^{\mathrm{3}} {x}−\mathrm{tan}^{\mathrm{3}} {x}+\mathrm{tan}^{\mathrm{5}} {x}}{\mathrm{1}−\mathrm{tan}\:^{\mathrm{2}} {x}−\mathrm{3tan}\:^{\mathrm{2}} {x}+\mathrm{3tan}\:^{\mathrm{4}} {x}−\mathrm{6tan}^{\mathrm{2}} \:{x}+\mathrm{2tan}^{\mathrm{4}} {x}} \\ $$$$=\frac{\mathrm{tan}\:^{\mathrm{5}} {x}−\mathrm{10tan}\:^{\mathrm{3}} {x}+\mathrm{5tan}\:{x}}{\mathrm{1}−\mathrm{10tan}\:^{\mathrm{2}} {x}+\mathrm{5tan}\:^{\mathrm{4}} {x}} \\ $$
Commented by mohammad17 last updated on 24/Nov/20
thank you sir
$${thank}\:{you}\:{sir} \\ $$
Answered by som(math1967) last updated on 24/Nov/20
cot5x =(1/(tan(3x+2x)))=((1−tan3xtan2x)/(tan 3x+tan 2x)) =((1−(((3tanx−tan^3 x)(2tanx))/((1−3tan^2 x)(1−tan^2 x))))/(((3tanx−tan^3 x)/(1−3tan^2 x))+((2tanx)/(1−tan^2 x)))) let tanx=a (((1−3a^2 )(1−a^2 )−6a^2 +2a^4 )/((1−a^2 )(3a−a^3 )+2a−6a^3 )) =((1−a^2 −3a^2 +3a^4 −6a^2 +2a^4 )/(3a−a^3 −3a^3 +a^5 +2a−6a^3 )) =((1−10a^2 +5a^4 )/(5a−10a^3 +a^5 )) now put a=tanx
$$\mathrm{cot5x} \\ $$$$=\frac{\mathrm{1}}{\mathrm{tan}\left(\mathrm{3x}+\mathrm{2x}\right)}=\frac{\mathrm{1}−\mathrm{tan3xtan2x}}{\mathrm{tan}\:\mathrm{3x}+\mathrm{tan}\:\mathrm{2x}} \\ $$$$=\frac{\mathrm{1}−\frac{\left(\mathrm{3tanx}−\mathrm{tan}^{\mathrm{3}} \mathrm{x}\right)\left(\mathrm{2tanx}\right)}{\left(\mathrm{1}−\mathrm{3tan}^{\mathrm{2}} \mathrm{x}\right)\left(\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \mathrm{x}\right)}}{\frac{\mathrm{3tanx}−\mathrm{tan}^{\mathrm{3}} \mathrm{x}}{\mathrm{1}−\mathrm{3tan}^{\mathrm{2}} \mathrm{x}}+\frac{\mathrm{2tanx}}{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \mathrm{x}}} \\ $$$$\mathrm{let}\:\mathrm{tanx}=\mathrm{a} \\ $$$$\frac{\left(\mathrm{1}−\mathrm{3a}^{\mathrm{2}} \right)\left(\mathrm{1}−\mathrm{a}^{\mathrm{2}} \right)−\mathrm{6a}^{\mathrm{2}} +\mathrm{2a}^{\mathrm{4}} }{\left(\mathrm{1}−\mathrm{a}^{\mathrm{2}} \right)\left(\mathrm{3a}−\mathrm{a}^{\mathrm{3}} \right)+\mathrm{2a}−\mathrm{6a}^{\mathrm{3}} } \\ $$$$=\frac{\mathrm{1}−\mathrm{a}^{\mathrm{2}} −\mathrm{3a}^{\mathrm{2}} +\mathrm{3a}^{\mathrm{4}} −\mathrm{6a}^{\mathrm{2}} +\mathrm{2a}^{\mathrm{4}} }{\mathrm{3a}−\mathrm{a}^{\mathrm{3}} −\mathrm{3a}^{\mathrm{3}} +\mathrm{a}^{\mathrm{5}} +\mathrm{2a}−\mathrm{6a}^{\mathrm{3}} } \\ $$$$=\frac{\mathrm{1}−\mathrm{10a}^{\mathrm{2}} +\mathrm{5a}^{\mathrm{4}} }{\mathrm{5a}−\mathrm{10a}^{\mathrm{3}} +\mathrm{a}^{\mathrm{5}} } \\ $$$$\mathrm{now}\:\mathrm{put}\:\mathrm{a}=\mathrm{tanx} \\ $$
Commented by mohammad17 last updated on 24/Nov/20
thank you sir
$${thank}\:{you}\:{sir} \\ $$
Answered by TANMAY PANACEA last updated on 24/Nov/20
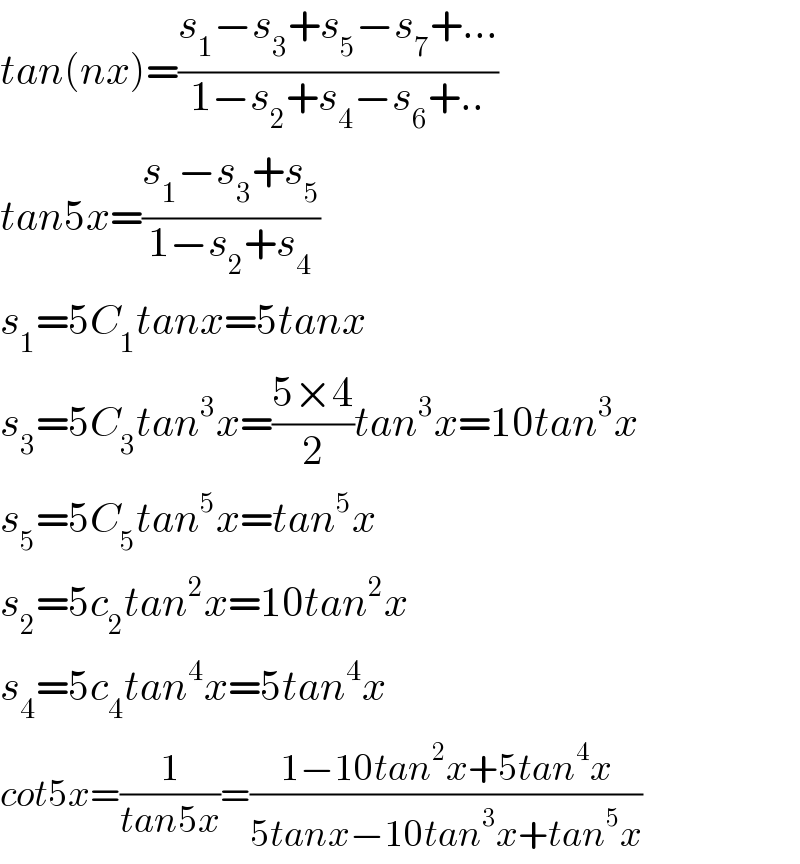
tan(nx)=((s_1 −s_3 +s_5 −s_7 +...)/(1−s_2 +s_4 −s_6 +..)) tan5x=((s_1 −s_3 +s_5 )/(1−s_2 +s_4 )) s_1 =5C_1 tanx=5tanx s_3 =5C_3 tan^3 x=((5×4)/2)tan^3 x=10tan^3 x s_5 =5C_5 tan^5 x=tan^5 x s_2 =5c_2 tan^2 x=10tan^2 x s_4 =5c_4 tan^4 x=5tan^4 x cot5x=(1/(tan5x))=((1−10tan^2 x+5tan^4 x)/(5tanx−10tan^3 x+tan^5 x))
$${tan}\left({nx}\right)=\frac{{s}_{\mathrm{1}} −{s}_{\mathrm{3}} +{s}_{\mathrm{5}} −{s}_{\mathrm{7}} +…}{\mathrm{1}−{s}_{\mathrm{2}} +{s}_{\mathrm{4}} −{s}_{\mathrm{6}} +..} \\ $$$${tan}\mathrm{5}{x}=\frac{{s}_{\mathrm{1}} −{s}_{\mathrm{3}} +{s}_{\mathrm{5}} }{\mathrm{1}−{s}_{\mathrm{2}} +{s}_{\mathrm{4}} } \\ $$$${s}_{\mathrm{1}} =\mathrm{5}{C}_{\mathrm{1}} {tanx}=\mathrm{5}{tanx} \\ $$$${s}_{\mathrm{3}} =\mathrm{5}{C}_{\mathrm{3}} {tan}^{\mathrm{3}} {x}=\frac{\mathrm{5}×\mathrm{4}}{\mathrm{2}}{tan}^{\mathrm{3}} {x}=\mathrm{10}{tan}^{\mathrm{3}} {x} \\ $$$${s}_{\mathrm{5}} =\mathrm{5}{C}_{\mathrm{5}} {tan}^{\mathrm{5}} {x}={tan}^{\mathrm{5}} {x} \\ $$$${s}_{\mathrm{2}} =\mathrm{5}{c}_{\mathrm{2}} {tan}^{\mathrm{2}} {x}=\mathrm{10}{tan}^{\mathrm{2}} {x} \\ $$$${s}_{\mathrm{4}} =\mathrm{5}{c}_{\mathrm{4}} {tan}^{\mathrm{4}} {x}=\mathrm{5}{tan}^{\mathrm{4}} {x} \\ $$$${cot}\mathrm{5}{x}=\frac{\mathrm{1}}{{tan}\mathrm{5}{x}}=\frac{\mathrm{1}−\mathrm{10}{tan}^{\mathrm{2}} {x}+\mathrm{5}{tan}^{\mathrm{4}} {x}}{\mathrm{5}{tanx}−\mathrm{10}{tan}^{\mathrm{3}} {x}+{tan}^{\mathrm{5}} {x}} \\ $$
Commented by som(math1967) last updated on 25/Nov/20
Nice sir
$$\mathrm{Nice}\:\mathrm{sir}\: \\ $$
Commented by som(math1967) last updated on 25/Nov/20
খুব ভাল
Commented by TANMAY PANACEA last updated on 25/Nov/20
thank you...
$${thank}\:{you}… \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *