Prove-that-d-dx-e-x-e-x-

Question Number 97972 by Aniruddha Ghosh last updated on 10/Jun/20

Prove that,

\frac{d}{d x} (e^{x}) = e^{x}

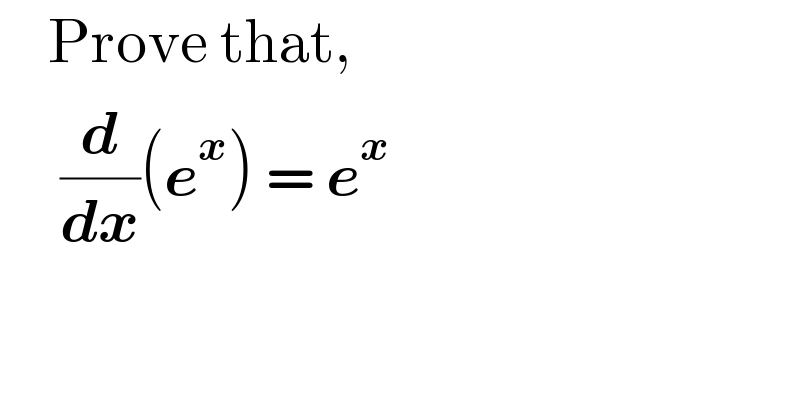
Answered by abdomathmax last updated on 10/Jun/20

\frac{d}{dx} (e^{x}) = \lim_{h \to 0} \frac{e^{x + h} - e^{x}}{h}

= \lim_{h \to 0} e^{x} \times \frac{e^{h} - 1}{h}

we have e^{h} = 1 + h + o (h^{2}) \Rightarrow e^{h} - 1 = h + o (h^{2}) \Rightarrow

\frac{e^{h} - 1}{h} = 1 + o (h) \Rightarrow \lim_{h \to 0} \frac{e^{h} - 1}{h} = 1 \Rightarrow

\frac{d}{dx} (e^{x}) = e^{x}

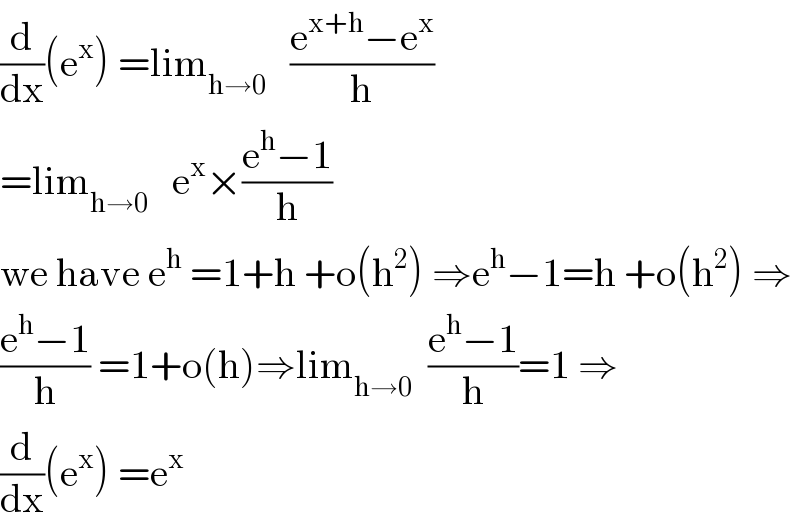
Answered by MJS last updated on 10/Jun/20

\frac{d}{d x} [f (x)] = \lim_{h \to 0} \frac{f (x + h) - f (x - h)}{2 h}

\frac{d}{d x} [e^{x}] = \lim_{h \to 0} \frac{e^{x + h} - e^{x - h}}{2 h} = \lim_{h \to 0} \frac{e^{h} - e^{- h}}{2 h} e^{x} =

= e^{x} \times \lim_{h \to 0} \frac{\sinh h}{h} =

[l^{'} Hopital]

= e^{x} \times \lim_{h \to 0} \frac{\frac{d}{d h} [\sinh h]}{\frac{d}{d h} [h]} = e^{x} \times \lim_{h \to 0} \cosh h = e^{x}

Answered by smridha last updated on 10/Jun/20

(i) \frac{d}{d x} (e^{x}) = \lim_{h \to 0} \frac{e^{x + h} - e^{x}}{h} [j u s t u s i n g t h e d e f i n e t i o n]

[t h a t \frac{d f}{d x} = \lim_{h \to 0} \frac{f (x + h) - f (x)}{h}]

s o w e g e t :

= e^{x} [\lim_{h \to 0} \frac{e^{h} - 1}{h}] = e^{x} . 1 = e^{x} .

(i i) n o w d o i t b y s e r i e s e x p a n s s i o n

e^{x} = \underset{n = 0}{\sum^{\infty}} \frac{x^{n}}{n!} = 1 + \frac{x}{1!} + \frac{x^{2}}{2!} + \frac{x^{3}}{3!} + \dots . . + \frac{x^{n}}{n!} + \frac{x^{n + 1}}{(n + 1)!} + \dots . \infty

n o w d i f f : w r t x w e g e t

\frac{d}{d x} (e^{x}) = 0 + [1 + \frac{x}{1!} + \frac{x^{2}}{2!} + \frac{x^{3}}{3!} + \dots + \frac{x^{n - 1}}{(n - 1)!} + \frac{x^{n}}{n!} + \dots \infty]

= 0 + e^{x} = e^{x} [i t s r e m a i n t h e a s i t i s]

Commented by MathGod last updated on 10/Jun/20

I USE THE REDDEST INK!

Commented by arcana last updated on 11/Jun/20

using e^{h} - 1 - h ⩾ 0, \forall h \in R

then 1 ⩽ \frac{e^{h} - 1}{h} ⩽ 1

\lim_{h \to 0} \frac{e^{h} - 1}{h} = 1

Facebook Tweet Pin