Question Number 166331 by mr W last updated on 18/Feb/22
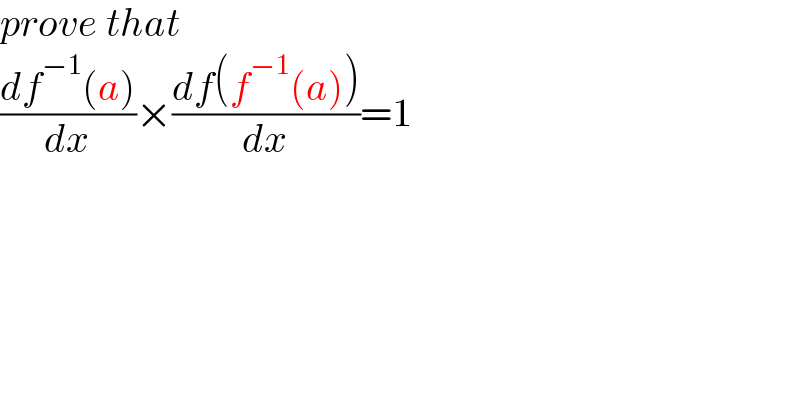
$${prove}\:{that} \\ $$$$\frac{{df}^{−\mathrm{1}} \left({a}\right)}{{dx}}×\frac{{df}\left({f}^{−\mathrm{1}} \left({a}\right)\right)}{{dx}}=\mathrm{1} \\ $$
Commented by mr W last updated on 19/Feb/22
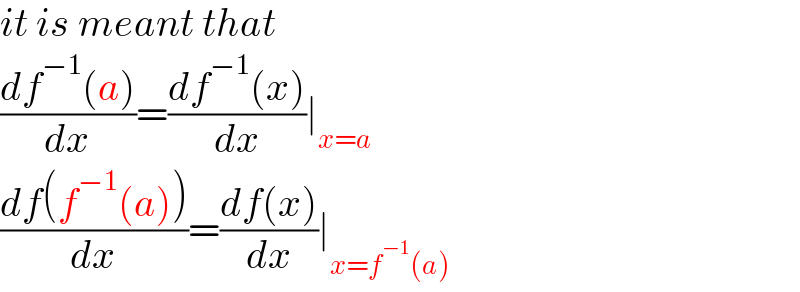
$${it}\:{is}\:{meant}\:{that} \\ $$$$\frac{{df}^{−\mathrm{1}} \left({a}\right)}{{dx}}=\frac{{df}^{−\mathrm{1}} \left({x}\right)}{{dx}}\mid_{{x}={a}} \\ $$$$\frac{{df}\left({f}^{−\mathrm{1}} \left({a}\right)\right)}{{dx}}=\frac{{df}\left({x}\right)}{{dx}}\mid_{{x}={f}^{−\mathrm{1}} \left({a}\right)} \\ $$
Answered by mathsmine last updated on 18/Feb/22
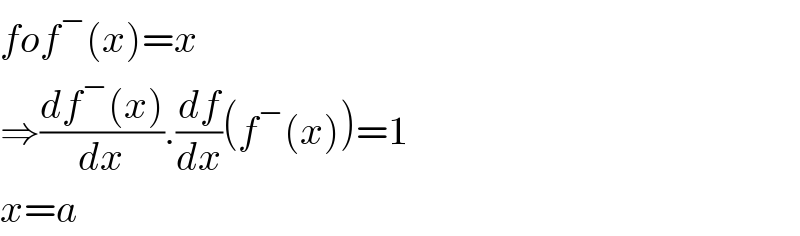
$${fof}^{−} \left({x}\right)={x} \\ $$$$\Rightarrow\frac{{df}^{−} \left({x}\right)}{{dx}}.\frac{{df}}{{dx}}\left({f}^{−} \left({x}\right)\right)=\mathrm{1} \\ $$$${x}={a} \\ $$
Commented by mr W last updated on 18/Feb/22

$${thanks}\:{sir}! \\ $$
Answered by mr W last updated on 19/Feb/22
Commented by mr W last updated on 18/Feb/22
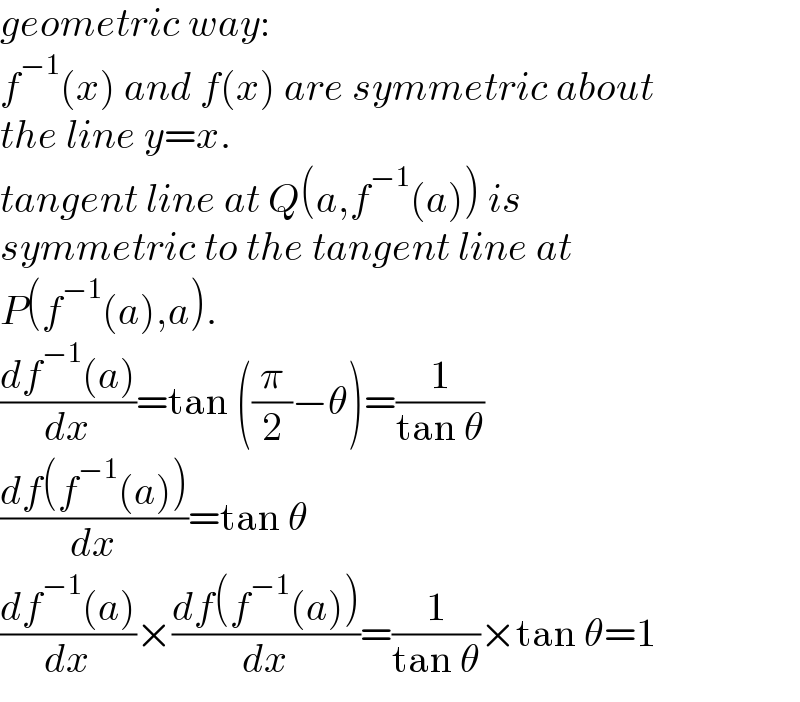
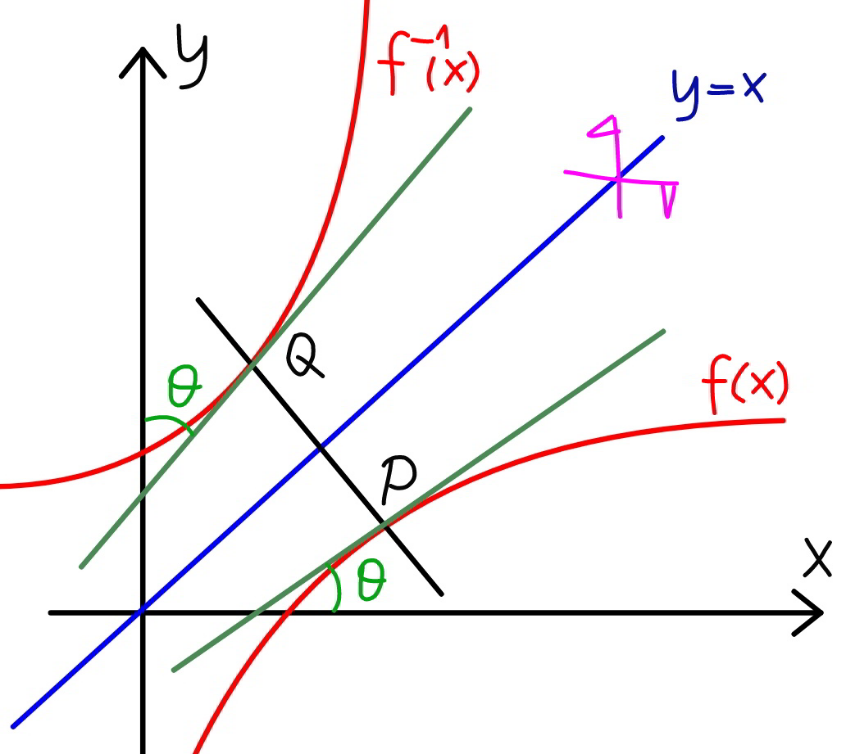
$${geometric}\:{way}: \\ $$$${f}^{−\mathrm{1}} \left({x}\right)\:{and}\:{f}\left({x}\right)\:{are}\:{symmetric}\:{about} \\ $$$${the}\:{line}\:{y}={x}.\: \\ $$$${tangent}\:{line}\:{at}\:{Q}\left({a},{f}^{−\mathrm{1}} \left({a}\right)\right)\:{is}\: \\ $$$${symmetric}\:{to}\:{the}\:{tangent}\:{line}\:{at} \\ $$$${P}\left({f}^{−\mathrm{1}} \left({a}\right),{a}\right). \\ $$$$\frac{{df}^{−\mathrm{1}} \left({a}\right)}{{dx}}=\mathrm{tan}\:\left(\frac{\pi}{\mathrm{2}}−\theta\right)=\frac{\mathrm{1}}{\mathrm{tan}\:\theta} \\ $$$$\frac{{df}\left({f}^{−\mathrm{1}} \left({a}\right)\right)}{{dx}}=\mathrm{tan}\:\theta \\ $$$$\frac{{df}^{−\mathrm{1}} \left({a}\right)}{{dx}}×\frac{{df}\left({f}^{−\mathrm{1}} \left({a}\right)\right)}{{dx}}=\frac{\mathrm{1}}{\mathrm{tan}\:\theta}×\mathrm{tan}\:\theta=\mathrm{1} \\ $$
