Question Number 147183 by mathdanisur last updated on 18/Jul/21
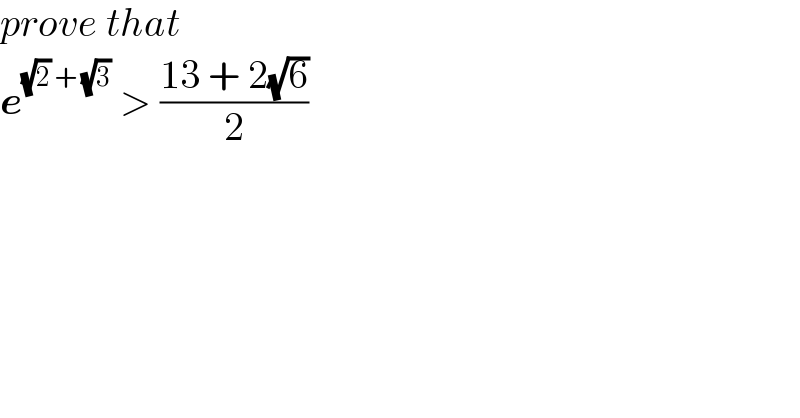
$${prove}\:{that} \\ $$$$\boldsymbol{{e}}^{\sqrt{\mathrm{2}}\:+\:\sqrt{\mathrm{3}}} \:>\:\frac{\mathrm{13}\:+\:\mathrm{2}\sqrt{\mathrm{6}}}{\mathrm{2}} \\ $$
Answered by mindispower last updated on 18/Jul/21
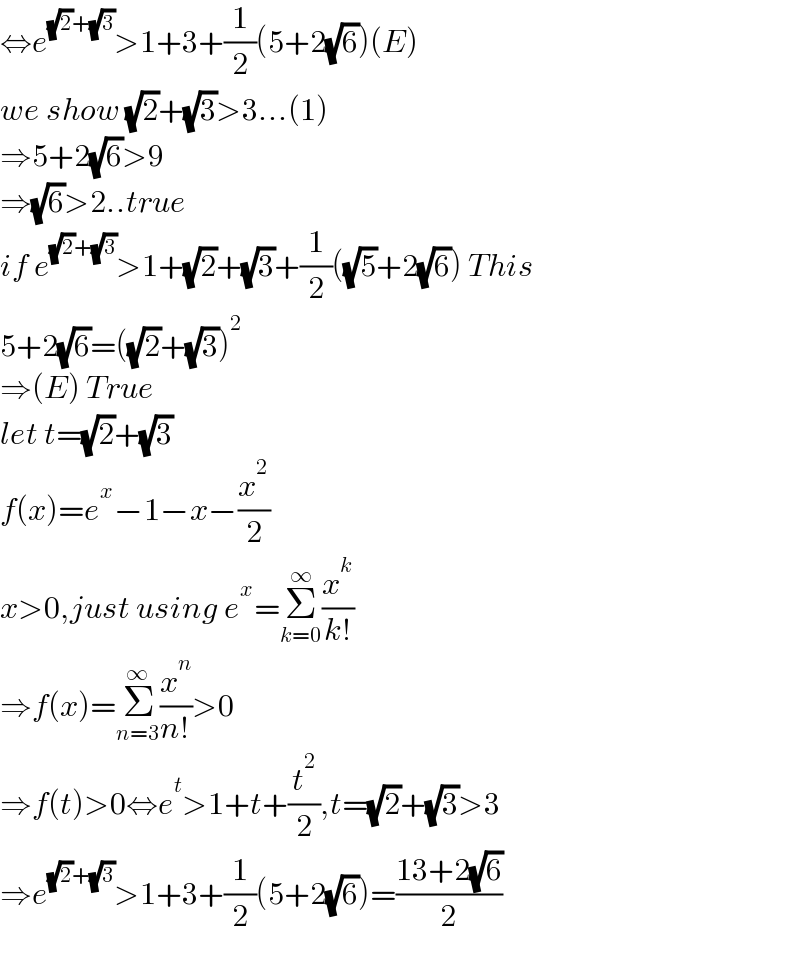
$$\Leftrightarrow{e}^{\sqrt{\mathrm{2}}+\sqrt{\mathrm{3}}} >\mathrm{1}+\mathrm{3}+\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{5}+\mathrm{2}\sqrt{\mathrm{6}}\right)\left({E}\right) \\ $$$${we}\:{show}\:\sqrt{\mathrm{2}}+\sqrt{\mathrm{3}}>\mathrm{3}…\left(\mathrm{1}\right) \\ $$$$\Rightarrow\mathrm{5}+\mathrm{2}\sqrt{\mathrm{6}}>\mathrm{9} \\ $$$$\Rightarrow\sqrt{\mathrm{6}}>\mathrm{2}..{true} \\ $$$${if}\:{e}^{\sqrt{\mathrm{2}}+\sqrt{\mathrm{3}}} >\mathrm{1}+\sqrt{\mathrm{2}}+\sqrt{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{2}}\left(\sqrt{\mathrm{5}}+\mathrm{2}\sqrt{\mathrm{6}}\right)\:{This} \\ $$$$\mathrm{5}+\mathrm{2}\sqrt{\mathrm{6}}=\left(\sqrt{\mathrm{2}}+\sqrt{\mathrm{3}}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\left({E}\right)\:{True} \\ $$$${let}\:{t}=\sqrt{\mathrm{2}}+\sqrt{\mathrm{3}} \\ $$$${f}\left({x}\right)={e}^{{x}} −\mathrm{1}−{x}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}} \\ $$$${x}>\mathrm{0},{just}\:{using}\:{e}^{{x}} =\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{x}^{{k}} }{{k}!} \\ $$$$\Rightarrow{f}\left({x}\right)=\underset{{n}=\mathrm{3}} {\overset{\infty} {\sum}}\frac{{x}^{{n}} }{{n}!}>\mathrm{0} \\ $$$$\Rightarrow{f}\left({t}\right)>\mathrm{0}\Leftrightarrow{e}^{{t}} >\mathrm{1}+{t}+\frac{{t}^{\mathrm{2}} }{\mathrm{2}},{t}=\sqrt{\mathrm{2}}+\sqrt{\mathrm{3}}>\mathrm{3} \\ $$$$\Rightarrow{e}^{\sqrt{\mathrm{2}}+\sqrt{\mathrm{3}}} >\mathrm{1}+\mathrm{3}+\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{5}+\mathrm{2}\sqrt{\mathrm{6}}\right)=\frac{\mathrm{13}+\mathrm{2}\sqrt{\mathrm{6}}}{\mathrm{2}} \\ $$$$ \\ $$
Commented by mathdanisur last updated on 19/Jul/21

$${thanks}\:{Ser}\:{cool} \\ $$
Commented by mindispower last updated on 19/Jul/21

$${withe}\:{pleasur} \\ $$
