Question Number 55364 by peter frank last updated on 22/Feb/19
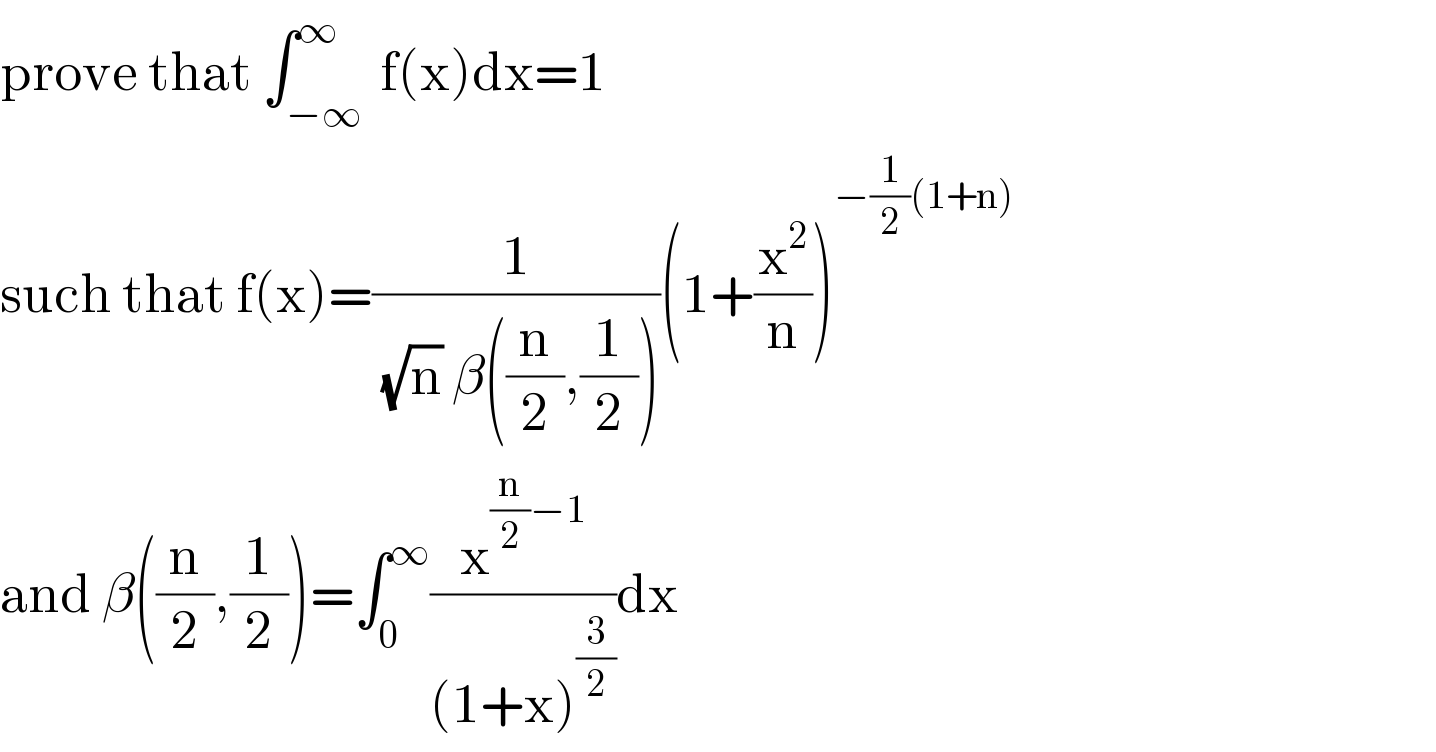
$$\mathrm{prove}\:\mathrm{that}\:\int_{−\infty\:} ^{\infty} \mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}=\mathrm{1} \\ $$$$\mathrm{such}\:\mathrm{that}\:\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{1}}{\:\sqrt{\mathrm{n}}\:\beta\left(\frac{\mathrm{n}}{\mathrm{2}},\frac{\mathrm{1}}{\mathrm{2}}\right)}\left(\mathrm{1}+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{n}}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+\mathrm{n}\right)} \\ $$$$\mathrm{and}\:\beta\left(\frac{\mathrm{n}}{\mathrm{2}},\frac{\mathrm{1}}{\mathrm{2}}\right)=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{x}^{\frac{\mathrm{n}}{\mathrm{2}}−\mathrm{1}} }{\left(\mathrm{1}+\mathrm{x}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} }\mathrm{dx} \\ $$
