prove-that-for-every-positivenumber-p-e-q-wee-have-p-q-4pq-

Question Number 181099 by Ari last updated on 21/Nov/22

prove that for every

positivenumber p e q wee

hav e :

p + q ⩾ \sqrt{4 p q}

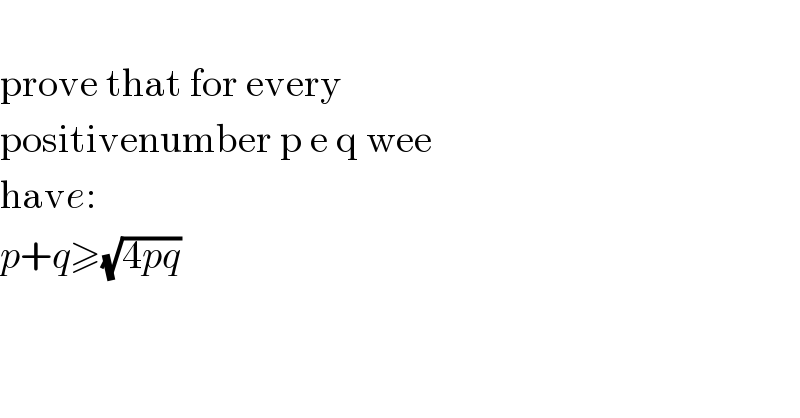
Answered by Agnibhoo98 last updated on 21/Nov/22

When p and q are positive numbers

{(p - q)}^{2} ⩾ 0

or p^{2} - 2 p q + q^{2} ⩾ 0

or p^{2} - 2 p q + 4 p q + q^{2} ⩾ 4 p q (Adding 4 p q both side)

or p^{2} + 2 p q + q^{2} ⩾ 4 p q

or {(p + q)}^{2} ⩾ 4 p q

or p + q ⩾ \sqrt{4 p q} (Proved)

Commented by Ari last updated on 21/Nov/22

T h a n k s M r \int!

Commented by Agnibhoo98 last updated on 22/Nov/22

Another way

According to AM ⩾ GM method :

\frac{p + q}{2} ⩾ \sqrt{p q}

or p + q ⩾ 2 \sqrt{p q}

or p + q ⩾ \sqrt{4 p q} (Proved)

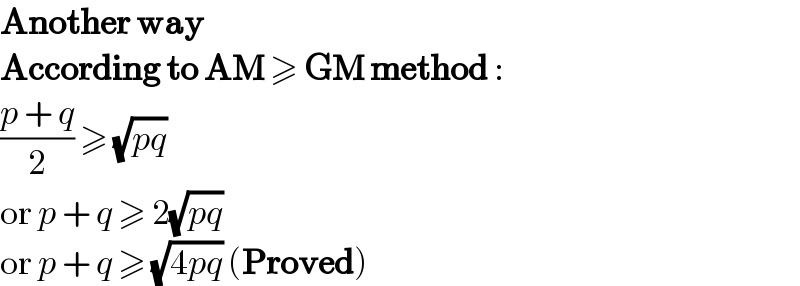
Answered by SEKRET last updated on 22/Nov/22

{(\sqrt{p} - \sqrt{q})}^{2} ⩾ 0

p + q ⩾ \sqrt{4 pq}

Facebook Tweet Pin