Question Number 54517 by hassentimol last updated on 05/Feb/19
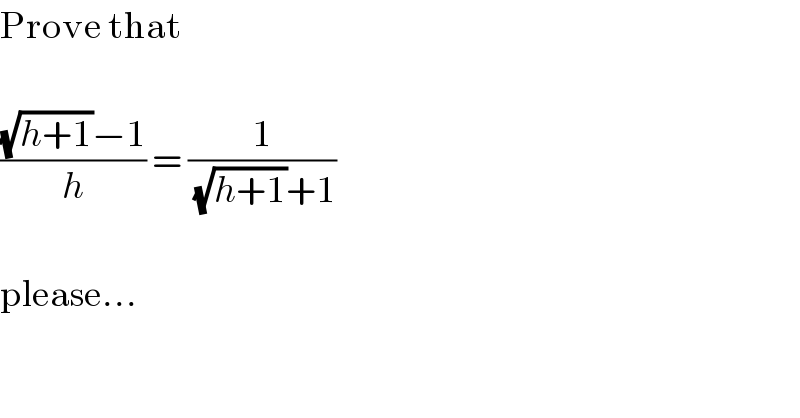
$$\mathrm{Prove}\:\mathrm{that} \\ $$$$ \\ $$$$\frac{\sqrt{{h}+\mathrm{1}}−\mathrm{1}}{{h}}\:=\:\frac{\mathrm{1}}{\:\sqrt{{h}+\mathrm{1}}+\mathrm{1}} \\ $$$$ \\ $$$$\mathrm{please}… \\ $$
Answered by Kunal12588 last updated on 05/Feb/19
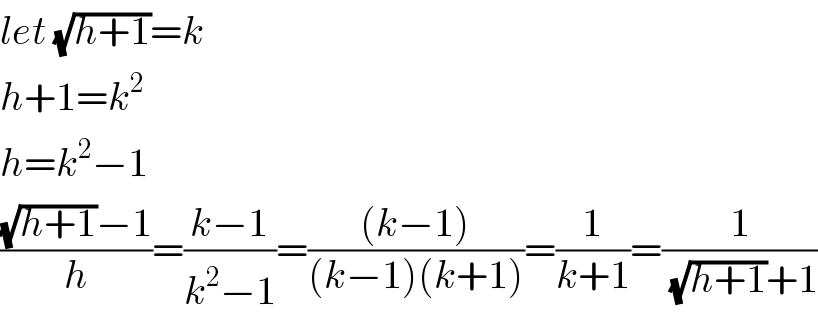
$${let}\:\sqrt{{h}+\mathrm{1}}={k} \\ $$$${h}+\mathrm{1}={k}^{\mathrm{2}} \\ $$$${h}={k}^{\mathrm{2}} −\mathrm{1} \\ $$$$\frac{\sqrt{{h}+\mathrm{1}}−\mathrm{1}}{{h}}=\frac{{k}−\mathrm{1}}{{k}^{\mathrm{2}} −\mathrm{1}}=\frac{\left({k}−\mathrm{1}\right)}{\left({k}−\mathrm{1}\right)\left({k}+\mathrm{1}\right)}=\frac{\mathrm{1}}{{k}+\mathrm{1}}=\frac{\mathrm{1}}{\:\sqrt{{h}+\mathrm{1}}+\mathrm{1}} \\ $$
Commented by hassentimol last updated on 05/Feb/19

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{Sir} \\ $$$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you} \\ $$
Answered by math1967 last updated on 05/Feb/19
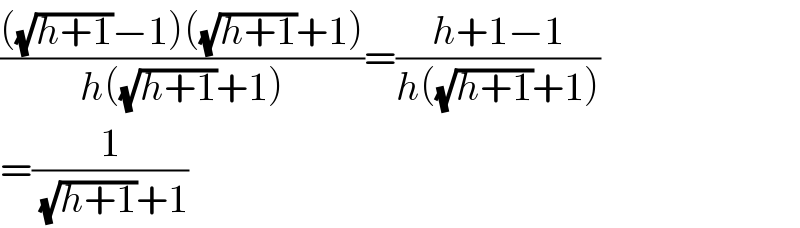
$$\frac{\left(\sqrt{{h}+\mathrm{1}}−\mathrm{1}\right)\left(\sqrt{{h}+\mathrm{1}}+\mathrm{1}\right)}{{h}\left(\sqrt{{h}+\mathrm{1}}+\mathrm{1}\right)}=\frac{{h}+\mathrm{1}−\mathrm{1}}{{h}\left(\sqrt{{h}+\mathrm{1}}+\mathrm{1}\right)} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{{h}+\mathrm{1}}+\mathrm{1}} \\ $$
Commented by hassentimol last updated on 05/Feb/19

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{Sir} \\ $$
