Menu Close

prove-that-i-0-1-x-s-1-1-x-dx-s-s-2-ln-2-ii-2x-1-2-x-1-2-x-1-2-ln-2-

Tinku Tara 0 Comments
Pin




Question Number 125297 by mnjuly1970 last updated on 09/Dec/20
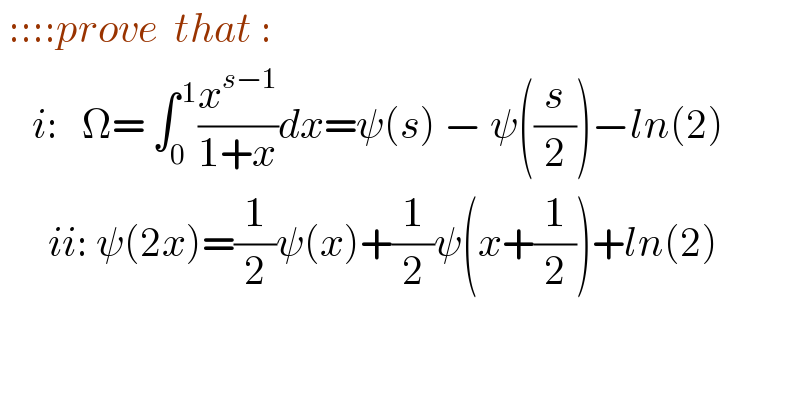
::::prove that : i: Ω= ∫_0 ^( 1) (x^(s−1) /(1+x))dx=ψ(s) − ψ((s/2))−ln(2) ii: ψ(2x)=(1/2)ψ(x)+(1/2)ψ(x+(1/2))+ln(2)
$$\:::::{prove}\:\:{that}\:: \\ $$$$\:\:\:\:{i}:\:\:\:\Omega=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{{x}^{{s}−\mathrm{1}} }{\mathrm{1}+{x}}{dx}=\psi\left({s}\right)\:−\:\psi\left(\frac{{s}}{\mathrm{2}}\right)−{ln}\left(\mathrm{2}\right) \\ $$$$\:\:\:\:\:\:{ii}:\:\psi\left(\mathrm{2}{x}\right)=\frac{\mathrm{1}}{\mathrm{2}}\psi\left({x}\right)+\frac{\mathrm{1}}{\mathrm{2}}\psi\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)+{ln}\left(\mathrm{2}\right) \\ $$
Answered by Bird last updated on 09/Dec/20
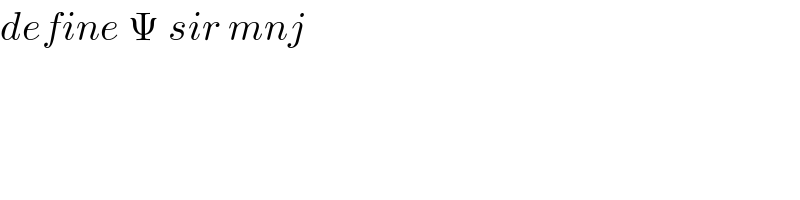
define Ψ sir mnj
$${define}\:\Psi\:{sir}\:{mnj} \\ $$
Commented by hatakekakashi1729gmailcom last updated on 10/Dec/20
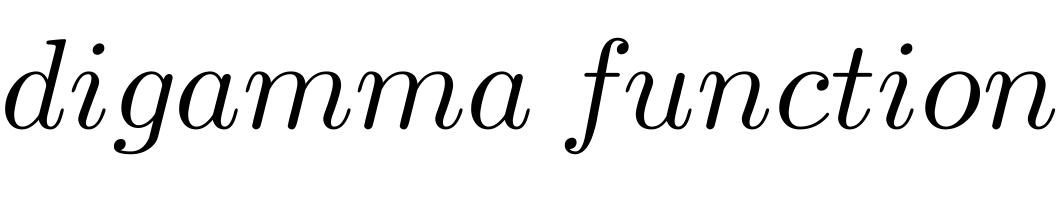
digamma function
$${digamma}\:{function} \\ $$
Commented by mnjuly1970 last updated on 10/Dec/20
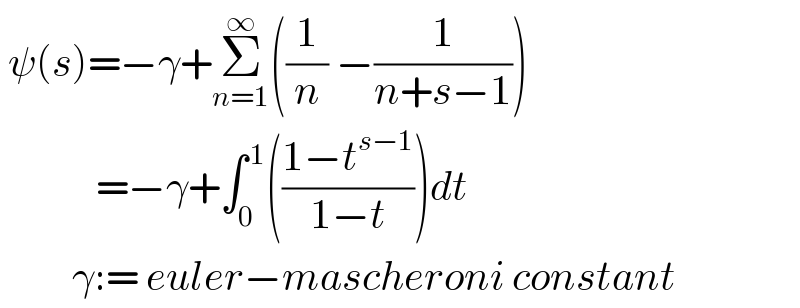
ψ(s)=−γ+Σ_(n=1) ^∞ ((1/n) −(1/(n+s−1))) =−γ+∫_0 ^( 1) (((1−t^(s−1) )/(1−t)))dt γ:= euler−mascheroni constant
$$\:\psi\left({s}\right)=−\gamma+\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{{n}}\:−\frac{\mathrm{1}}{{n}+{s}−\mathrm{1}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=−\gamma+\int_{\mathrm{0}} ^{\:\mathrm{1}} \left(\frac{\mathrm{1}−{t}^{{s}−\mathrm{1}} }{\mathrm{1}−{t}}\right){dt} \\ $$$$\:\:\:\:\:\:\:\:\:\gamma:=\:{euler}−{mascheroni}\:{constant} \\ $$
Commented by mnjuly1970 last updated on 10/Dec/20
thank you sir..
$${thank}\:{you}\:{sir}.. \\ $$
Answered by Dwaipayan Shikari last updated on 10/Dec/20
∫_0 ^1 (x^(s−1) /(1+x))dx = Σ_(n=0) ^∞ (−1)^n ∫_0 ^1 x^(s+n−1) =Σ_(n≥0) ^∞ (((−1)^n )/(n+s))
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{{s}−\mathrm{1}} }{\mathrm{1}+{x}}{dx}\:=\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} \int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{s}+{n}−\mathrm{1}} =\underset{{n}\geqslant\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}+{s}} \\ $$
Answered by mindispower last updated on 11/Dec/20
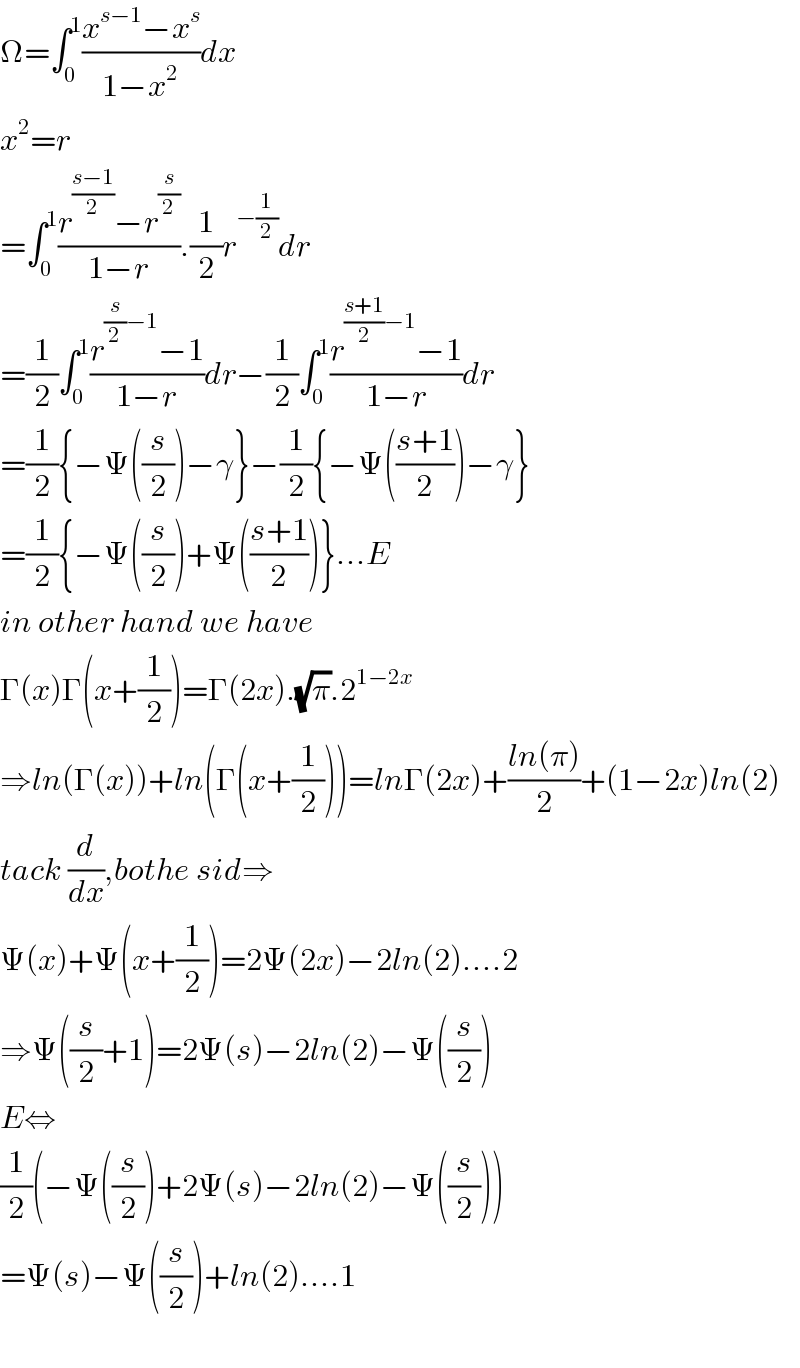
Ω=∫_0 ^1 ((x^(s−1) −x^s )/(1−x^2 ))dx x^2 =r =∫_0 ^1 ((r^((s−1)/2) −r^(s/2) )/(1−r)).(1/2)r^(−(1/2)) dr =(1/2)∫_0 ^1 ((r^((s/2)−1) −1)/(1−r))dr−(1/2)∫_0 ^1 ((r^(((s+1)/2)−1) −1)/(1−r))dr =(1/2){−Ψ((s/2))−γ}−(1/2){−Ψ(((s+1)/2))−γ} =(1/2){−Ψ((s/2))+Ψ(((s+1)/2))}...E in other hand we have Γ(x)Γ(x+(1/2))=Γ(2x).(√π).2^(1−2x) ⇒ln(Γ(x))+ln(Γ(x+(1/2)))=lnΓ(2x)+((ln(π))/2)+(1−2x)ln(2) tack (d/dx),bothe sid⇒ Ψ(x)+Ψ(x+(1/2))=2Ψ(2x)−2ln(2)....2 ⇒Ψ((s/2)+1)=2Ψ(s)−2ln(2)−Ψ((s/2)) E⇔ (1/2)(−Ψ((s/2))+2Ψ(s)−2ln(2)−Ψ((s/2))) =Ψ(s)−Ψ((s/2))+ln(2)....1
$$\Omega=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{{s}−\mathrm{1}} −{x}^{{s}} }{\mathrm{1}−{x}^{\mathrm{2}} }{dx} \\ $$$${x}^{\mathrm{2}} ={r} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{r}^{\frac{{s}−\mathrm{1}}{\mathrm{2}}} −{r}^{\frac{{s}}{\mathrm{2}}} }{\mathrm{1}−{r}}.\frac{\mathrm{1}}{\mathrm{2}}{r}^{−\frac{\mathrm{1}}{\mathrm{2}}} {dr} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{r}^{\frac{{s}}{\mathrm{2}}−\mathrm{1}} −\mathrm{1}}{\mathrm{1}−{r}}{dr}−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{r}^{\frac{{s}+\mathrm{1}}{\mathrm{2}}−\mathrm{1}} −\mathrm{1}}{\mathrm{1}−{r}}{dr} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left\{−\Psi\left(\frac{{s}}{\mathrm{2}}\right)−\gamma\right\}−\frac{\mathrm{1}}{\mathrm{2}}\left\{−\Psi\left(\frac{{s}+\mathrm{1}}{\mathrm{2}}\right)−\gamma\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left\{−\Psi\left(\frac{{s}}{\mathrm{2}}\right)+\Psi\left(\frac{{s}+\mathrm{1}}{\mathrm{2}}\right)\right\}…{E} \\ $$$${in}\:{other}\:{hand}\:{we}\:{have} \\ $$$$\Gamma\left({x}\right)\Gamma\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)=\Gamma\left(\mathrm{2}{x}\right).\sqrt{\pi}.\mathrm{2}^{\mathrm{1}−\mathrm{2}{x}} \\ $$$$\Rightarrow{ln}\left(\Gamma\left({x}\right)\right)+{ln}\left(\Gamma\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)\right)={ln}\Gamma\left(\mathrm{2}{x}\right)+\frac{{ln}\left(\pi\right)}{\mathrm{2}}+\left(\mathrm{1}−\mathrm{2}{x}\right){ln}\left(\mathrm{2}\right) \\ $$$${tack}\:\frac{{d}}{{dx}},{bothe}\:{sid}\Rightarrow \\ $$$$\Psi\left({x}\right)+\Psi\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)=\mathrm{2}\Psi\left(\mathrm{2}{x}\right)−\mathrm{2}{ln}\left(\mathrm{2}\right)….\mathrm{2} \\ $$$$\Rightarrow\Psi\left(\frac{{s}}{\mathrm{2}}+\mathrm{1}\right)=\mathrm{2}\Psi\left({s}\right)−\mathrm{2}{ln}\left(\mathrm{2}\right)−\Psi\left(\frac{{s}}{\mathrm{2}}\right) \\ $$$${E}\Leftrightarrow \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left(−\Psi\left(\frac{{s}}{\mathrm{2}}\right)+\mathrm{2}\Psi\left({s}\right)−\mathrm{2}{ln}\left(\mathrm{2}\right)−\Psi\left(\frac{{s}}{\mathrm{2}}\right)\right) \\ $$$$=\Psi\left({s}\right)−\Psi\left(\frac{{s}}{\mathrm{2}}\right)+{ln}\left(\mathrm{2}\right)….\mathrm{1} \\ $$$$ \\ $$
Commented by mnjuly1970 last updated on 12/Dec/20
mercey sir..
$${mercey}\:{sir}.. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *