Question Number 151447 by mnjuly1970 last updated on 21/Aug/21
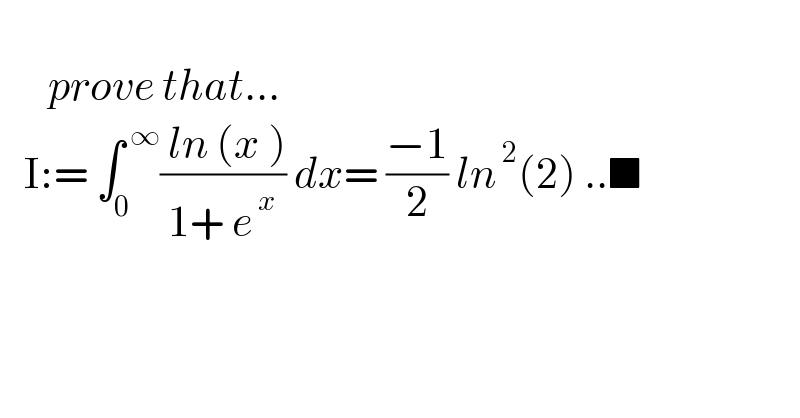
$$ \\ $$$$\:\:\:\:\:\:{prove}\:{that}… \\ $$$$\:\:\:\mathrm{I}:=\:\int_{\mathrm{0}} ^{\:\infty} \frac{\:{ln}\:\left({x}\:\right)}{\mathrm{1}+\:{e}^{\:{x}} }\:{dx}=\:\frac{−\mathrm{1}}{\mathrm{2}}\:{ln}^{\:\mathrm{2}} \left(\mathrm{2}\right)\:..\blacksquare \\ $$
Answered by Lordose last updated on 21/Aug/21
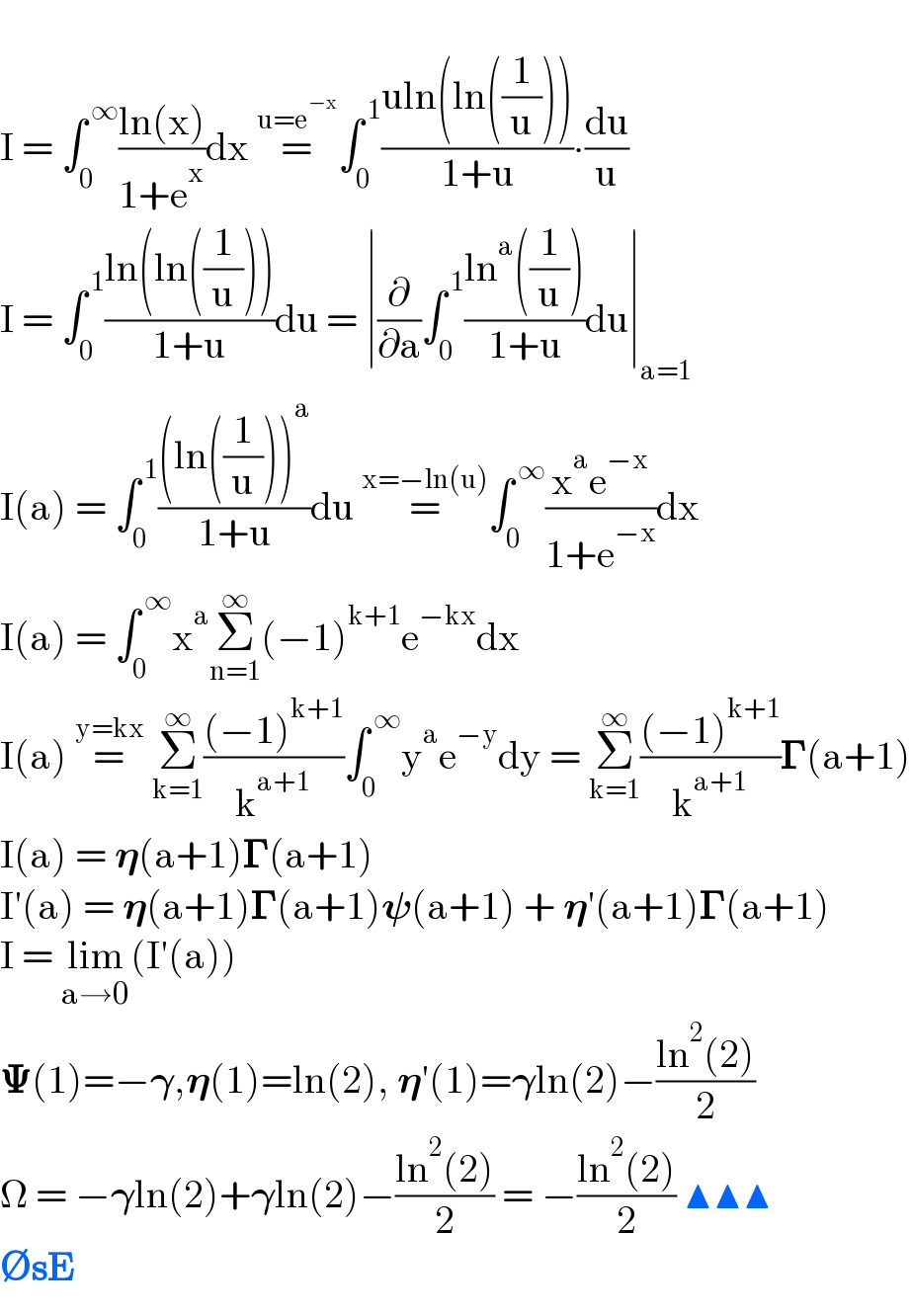
$$ \\ $$$$\mathrm{I}\:=\:\int_{\mathrm{0}} ^{\:\infty} \frac{\mathrm{ln}\left(\mathrm{x}\right)}{\mathrm{1}+\mathrm{e}^{\mathrm{x}} }\mathrm{dx}\:\overset{\mathrm{u}=\mathrm{e}^{−\mathrm{x}} } {=}\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{uln}\left(\mathrm{ln}\left(\frac{\mathrm{1}}{\mathrm{u}}\right)\right)}{\mathrm{1}+\mathrm{u}}\centerdot\frac{\mathrm{du}}{\mathrm{u}} \\ $$$$\mathrm{I}\:=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{ln}\left(\mathrm{ln}\left(\frac{\mathrm{1}}{\mathrm{u}}\right)\right)}{\mathrm{1}+\mathrm{u}}\mathrm{du}\:=\:\mid\frac{\partial}{\partial\mathrm{a}}\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{ln}^{\mathrm{a}} \left(\frac{\mathrm{1}}{\mathrm{u}}\right)}{\mathrm{1}+\mathrm{u}}\mathrm{du}\mid_{\mathrm{a}=\mathrm{1}} \\ $$$$\mathrm{I}\left(\mathrm{a}\right)\:=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\left(\mathrm{ln}\left(\frac{\mathrm{1}}{\mathrm{u}}\right)\right)^{\mathrm{a}} }{\mathrm{1}+\mathrm{u}}\mathrm{du}\:\overset{\mathrm{x}=−\mathrm{ln}\left(\mathrm{u}\right)} {=}\int_{\mathrm{0}} ^{\:\infty} \frac{\mathrm{x}^{\mathrm{a}} \mathrm{e}^{−\mathrm{x}} }{\mathrm{1}+\mathrm{e}^{−\mathrm{x}} }\mathrm{dx} \\ $$$$\mathrm{I}\left(\mathrm{a}\right)\:=\:\int_{\mathrm{0}} ^{\:\infty} \mathrm{x}^{\mathrm{a}} \underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{\mathrm{k}+\mathrm{1}} \mathrm{e}^{−\mathrm{kx}} \mathrm{dx} \\ $$$$\mathrm{I}\left(\mathrm{a}\right)\:\overset{\mathrm{y}=\mathrm{kx}} {=}\:\underset{\mathrm{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{\mathrm{k}+\mathrm{1}} }{\mathrm{k}^{\mathrm{a}+\mathrm{1}} }\int_{\mathrm{0}} ^{\:\infty} \mathrm{y}^{\mathrm{a}} \mathrm{e}^{−\mathrm{y}} \mathrm{dy}\:=\:\underset{\mathrm{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{\mathrm{k}+\mathrm{1}} }{\mathrm{k}^{\mathrm{a}+\mathrm{1}} }\boldsymbol{\Gamma}\left(\mathrm{a}+\mathrm{1}\right) \\ $$$$\mathrm{I}\left(\mathrm{a}\right)\:=\:\boldsymbol{\eta}\left(\mathrm{a}+\mathrm{1}\right)\boldsymbol{\Gamma}\left(\mathrm{a}+\mathrm{1}\right) \\ $$$$\mathrm{I}'\left(\mathrm{a}\right)\:=\:\boldsymbol{\eta}\left(\mathrm{a}+\mathrm{1}\right)\boldsymbol{\Gamma}\left(\mathrm{a}+\mathrm{1}\right)\boldsymbol{\psi}\left(\mathrm{a}+\mathrm{1}\right)\:+\:\boldsymbol{\eta}'\left(\mathrm{a}+\mathrm{1}\right)\boldsymbol{\Gamma}\left(\mathrm{a}+\mathrm{1}\right) \\ $$$$\mathrm{I}\:=\:\underset{\mathrm{a}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\mathrm{I}'\left(\mathrm{a}\right)\right) \\ $$$$\boldsymbol{\Psi}\left(\mathrm{1}\right)=−\boldsymbol{\gamma},\boldsymbol{\eta}\left(\mathrm{1}\right)=\mathrm{ln}\left(\mathrm{2}\right),\:\boldsymbol{\eta}'\left(\mathrm{1}\right)=\boldsymbol{\gamma}\mathrm{ln}\left(\mathrm{2}\right)−\frac{\mathrm{ln}^{\mathrm{2}} \left(\mathrm{2}\right)}{\mathrm{2}} \\ $$$$\Omega\:=\:−\boldsymbol{\gamma}\mathrm{ln}\left(\mathrm{2}\right)+\boldsymbol{\gamma}\mathrm{ln}\left(\mathrm{2}\right)−\frac{\mathrm{ln}^{\mathrm{2}} \left(\mathrm{2}\right)}{\mathrm{2}}\:=\:−\frac{\mathrm{ln}^{\mathrm{2}} \left(\mathrm{2}\right)}{\mathrm{2}}\:\blacktriangle\blacktriangle\blacktriangle \\ $$$$\boldsymbol{\varnothing\mathrm{sE}} \\ $$
Commented by mnjuly1970 last updated on 21/Aug/21
$${very}\:{nice}\:{master}\:{lordose}.. \\ $$
Commented by Tawa11 last updated on 22/Aug/21

$$\mathrm{And}\:\:\:\:\mathrm{Q151641} \\ $$
