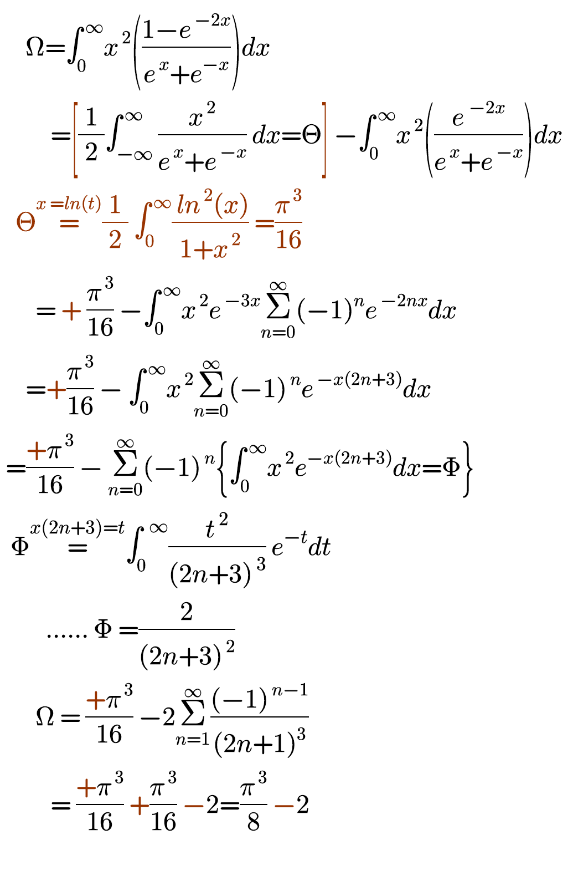Question Number 157961 by mnjuly1970 last updated on 30/Oct/21
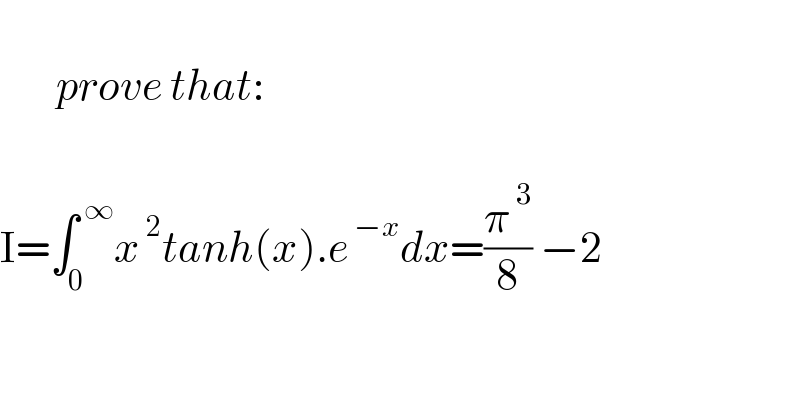
$$ \\ $$$$\:\:\:\:\:\:\:{prove}\:{that}: \\ $$$$ \\ $$$$\mathrm{I}=\int_{\mathrm{0}} ^{\:\infty} {x}^{\:\mathrm{2}} {tanh}\left({x}\right).{e}^{\:−{x}} {dx}=\frac{\pi^{\:\mathrm{3}} }{\mathrm{8}}\:−\mathrm{2}\:\:\:\:\:\:\: \\ $$$$ \\ $$
Answered by qaz last updated on 30/Oct/21
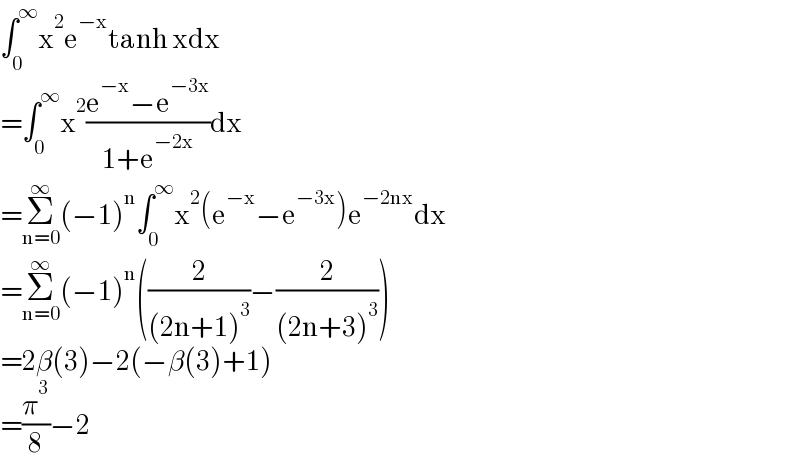
$$\int_{\mathrm{0}} ^{\infty} \mathrm{x}^{\mathrm{2}} \mathrm{e}^{−\mathrm{x}} \mathrm{tanh}\:\mathrm{xdx} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \mathrm{x}^{\mathrm{2}} \frac{\mathrm{e}^{−\mathrm{x}} −\mathrm{e}^{−\mathrm{3x}} }{\mathrm{1}+\mathrm{e}^{−\mathrm{2x}} }\mathrm{dx} \\ $$$$=\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{\mathrm{n}} \int_{\mathrm{0}} ^{\infty} \mathrm{x}^{\mathrm{2}} \left(\mathrm{e}^{−\mathrm{x}} −\mathrm{e}^{−\mathrm{3x}} \right)\mathrm{e}^{−\mathrm{2nx}} \mathrm{dx} \\ $$$$=\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{\mathrm{n}} \left(\frac{\mathrm{2}}{\left(\mathrm{2n}+\mathrm{1}\right)^{\mathrm{3}} }−\frac{\mathrm{2}}{\left(\mathrm{2n}+\mathrm{3}\right)^{\mathrm{3}} }\right) \\ $$$$=\mathrm{2}\beta\left(\mathrm{3}\right)−\mathrm{2}\left(−\beta\left(\mathrm{3}\right)+\mathrm{1}\right) \\ $$$$=\frac{\pi^{\mathrm{3}} }{\mathrm{8}}−\mathrm{2} \\ $$
Commented by mnjuly1970 last updated on 30/Oct/21
$${very}\:{nicd}\:{sir}\:{qaz} \\ $$
Answered by mnjuly1970 last updated on 30/Oct/21