Menu Close

Prove-that-if-z-cos-6-i-sin-6-then-1-z-2-1-iz-z-4-1-iz-3-z-8-1-iz-7-z-16-1-0-

Tinku Tara 0 Comments
Pin




Question Number 19455 by Tinkutara last updated on 11/Aug/17
Prove that if z = cos 6° + i sin 6°, then (1/(z^2 + 1)) − ((iz)/(z^4 − 1)) + ((iz^3 )/(z^8 − 1)) + ((iz^7 )/(z^(16) − 1)) = 0.
Provethatifz=cos6°+isin6°,then1z2+1−izz4−1+iz3z8−1+iz7z16−1=0.
Answered by ajfour last updated on 16/Aug/17
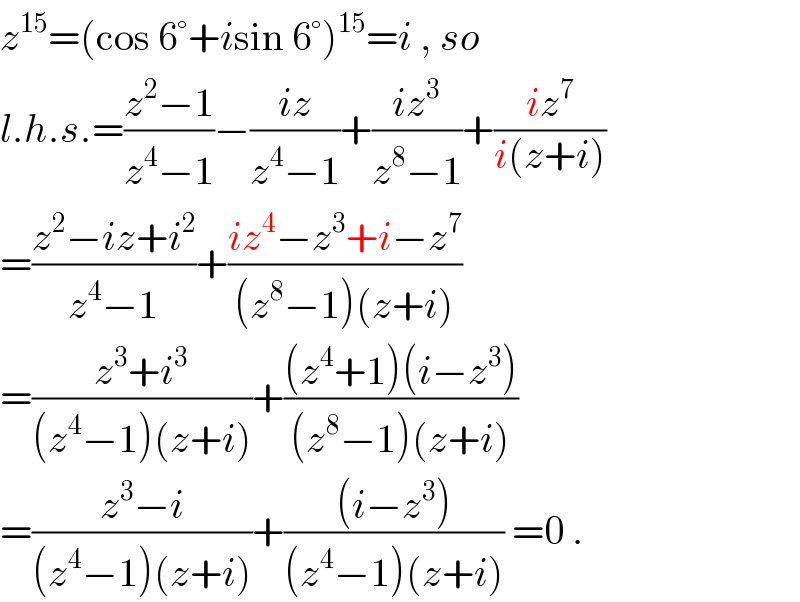
z^(15) =(cos 6°+isin 6°)^(15) =i , so l.h.s.=((z^2 −1)/(z^4 −1))−((iz)/(z^4 −1))+((iz^3 )/(z^8 −1))+((iz^7 )/(i(z+i))) =((z^2 −iz+i^2 )/(z^4 −1))+((iz^4 −z^3 +i−z^7 )/((z^8 −1)(z+i))) =((z^3 +i^3 )/((z^4 −1)(z+i)))+(((z^4 +1)(i−z^3 ))/((z^8 −1)(z+i))) =((z^3 −i)/((z^4 −1)(z+i)))+(((i−z^3 ))/((z^4 −1)(z+i))) =0 .
z15=(cos6°+isin6°)15=i,sol.h.s.=z2−1z4−1−izz4−1+iz3z8−1+iz7i(z+i)=z2−iz+i2z4−1+iz4−z3+i−z7(z8−1)(z+i)=z3+i3(z4−1)(z+i)+(z4+1)(i−z3)(z8−1)(z+i)=z3−i(z4−1)(z+i)+(i−z3)(z4−1)(z+i)=0.
Commented by Tinkutara last updated on 16/Aug/17
Thank you very much Sir!
ThankyouverymuchSir!

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *