Prove-that-k-0-n-1-2-n-1-n-2-n-1-

Question Number 183726 by LEKOUMA last updated on 29/Dec/22

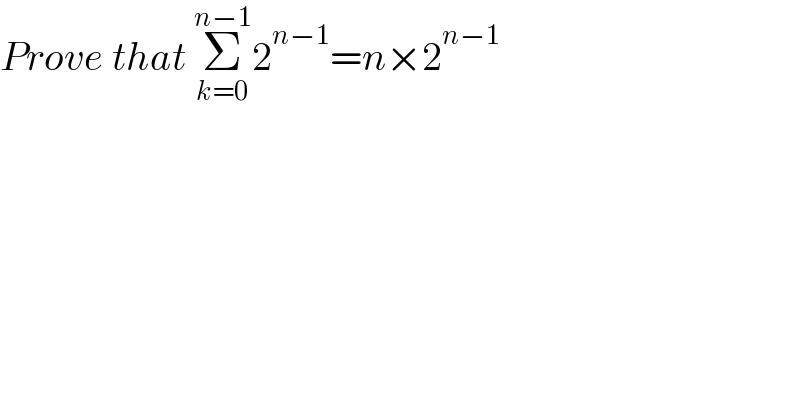
Prove that Σ_(k=0) ^(n−1) 2^(n−1) =n×2^(n−1)

$${Prove}\:{that}\:\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}\mathrm{2}^{{n}−\mathrm{1}} ={n}×\mathrm{2}^{{n}−\mathrm{1}} \: \\ $$

Commented by JDamian last updated on 29/Dec/22

seriously?

Answered by Vynho last updated on 29/Dec/22

it′s the sum of 2^(n−1) at [(n−1)+1] time

$${it}'{s}\:{the}\:{sum}\:{of}\:\:\mathrm{2}^{{n}−\mathrm{1}} \:{at}\:\left[\left({n}−\mathrm{1}\right)+\mathrm{1}\right]\:{time} \\ $$

Answered by Ar Brandon last updated on 29/Dec/22

Σ_(k=0) ^(n−1) 2^(n−1) =2^(n−1) Σ_(k=0) ^(n−1) (1)=2^(n−1) ×n=n×2^(n−1)

$$\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}\mathrm{2}^{{n}−\mathrm{1}} =\mathrm{2}^{{n}−\mathrm{1}} \underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}\left(\mathrm{1}\right)=\mathrm{2}^{{n}−\mathrm{1}} ×{n}={n}×\mathrm{2}^{{n}−\mathrm{1}} \\ $$

Facebook Tweet Pin

Prove-that-k-0-n-1-2-n-1-n-2-n-1-

Leave a Reply Cancel reply