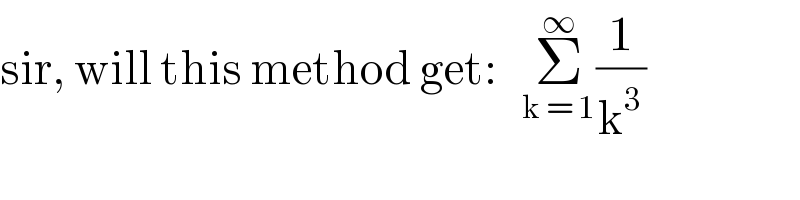Prove-that-k-1-1-k-2-pi-2-6-

Question Number 96667 by Ar Brandon last updated on 03/Jun/20

P rove that \underset{k = 1}{\sum^{\infty}} \frac{1}{k^{2}} = \frac{π^{2}}{6}

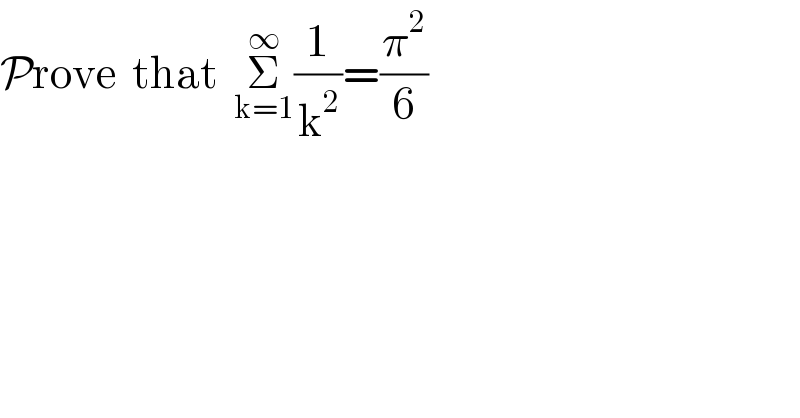
Answered by Sourav mridha last updated on 03/Jun/20

\underset{k = 1}{\sum^{\infty}} k^{- 2} = ζ (2)

f ro m t h e r e l a t i o n o f R i e m a n n

z e t a f^{n} w i t h B u r n o u l l i n u m b e r

(e v e n) .

B_{2 n} = {(- 1)}^{n - 1} \frac{2 (2 n)!}{{(2 π)}^{2 n}} . ζ (2 n) .

p u t . . n = 1

t h e n, B_{2} = \frac{2.2!}{2.2 . π^{2}} . ζ (2)

w e k n o w B_{2} = \frac{1}{6} . n o w p u t t i n g i t

w e g e t . . ζ (2) = \frac{π^{2}}{6} \dots

Commented by I want to learn more last updated on 05/Jun/20

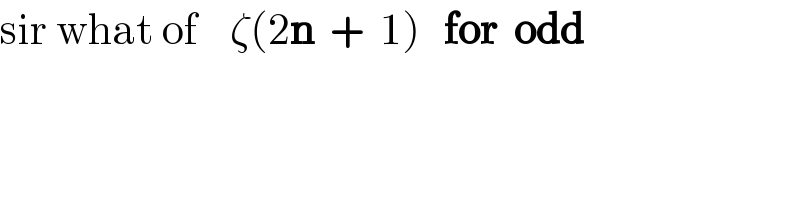
sir what of ζ (2 n + 1) for odd

Commented by Sourav mridha last updated on 05/Jun/20

T his i s n o t j u s t i f i e d b y t h i s

f o r m u l a b e c a u s e :

B_{2 n + 1} = 0 w h e r e n \in N

o n l y o d d n u m b e r B_{1} = - \frac{1}{2} e x i s t .

g e n e r e l f o r m o f B_{n} :

B_{n} = - \frac{n!}{{(2 π i)}^{n}} [\underset{m = 1}{\sum^{\infty}} (\frac{1}{m^{n}} + \frac{1}{{(- m)}^{n}})]

Commented by I want to learn more last updated on 06/Jun/20

Thanks sir

Answered by Rio Michael last updated on 03/Jun/20

i^{'} ve always W anted to G et this proof . . and {here}^{'} s what i fell on .

\underset{k = 1}{\sum^{\infty}} \frac{1}{k^{2}} = \frac{π^{2}}{6}

first let s = \arcsin x

hence {\int^{\frac{π}{2}}}_{0} s d s = \frac{π^{2}}{8}

also \int_{0}^{1} \frac{\arcsin x}{\sqrt{1 - x^{2}}} d x = \frac{π^{2}}{8}

since arc \sin x = \int_{0}^{1} \frac{1}{\sqrt{1 - x^{2}}} d x = x + \frac{x^{3}}{2 \times 3} + \frac{1 \times 3 x^{5}}{2 \times 5 \times 5} + \dots

substituting we get : \int_{0}^{1} (\frac{d x}{\sqrt{1 - x^{2}}} \int \frac{d x}{\sqrt{1 - x^{2}}}) = \int_{0}^{1} [x + \frac{x^{3}}{6} (\frac{d x}{\sqrt{1 - x^{2}}}) + \dots]

realise that : \int_{0}^{1} \frac{x^{2 n + 1}}{\sqrt{1 - x^{2}}} d x = \frac{2 n!!}{(2 n + 1)!!} . since we get all odd powers,

\frac{π^{2}}{8} = \underset{k = 1}{\sum^{\infty}} \frac{1}{{(2 n - 1)}^{2}}

if we define x = \underset{k = 1}{\sum^{\infty}} \frac{1}{k^{2}}

dividing by 4, we get the equation : x = \frac{π^{2}}{6} = \underset{k = 1}{\sum^{\infty}} \frac{1}{k^{2}}

please guys check .

Commented by Ar Brandon last updated on 03/Jun/20

I'm lost.��

Commented by I want to learn more last updated on 06/Jun/20

thanks sir

Commented by I want to learn more last updated on 06/Jun/20

sir, will this method get : \underset{k = 1}{\sum^{\infty}} \frac{1}{k^{3}}