Menu Close

prove-that-k-1-n-1-n-k-lt-ln-2-

Tinku Tara 0 Comments
Pin




Question Number 185024 by aba last updated on 15/Jan/23
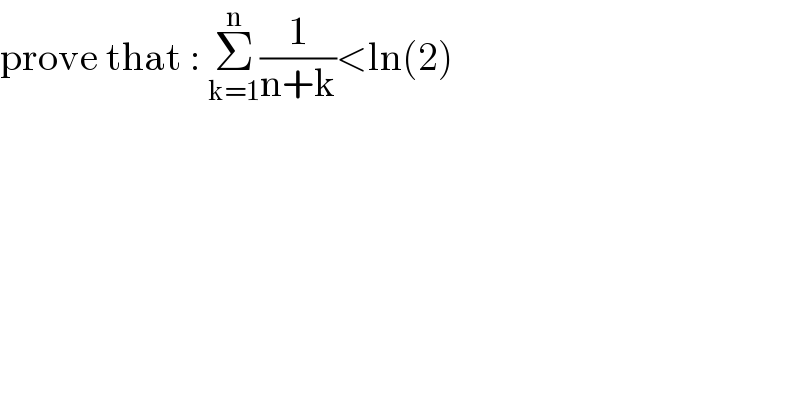
prove that : Σ_(k=1) ^n (1/(n+k))<ln(2)
$$\mathrm{prove}\:\mathrm{that}\::\:\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\frac{\mathrm{1}}{\mathrm{n}+\mathrm{k}}<\mathrm{ln}\left(\mathrm{2}\right) \\ $$
Answered by witcher3 last updated on 16/Jan/23
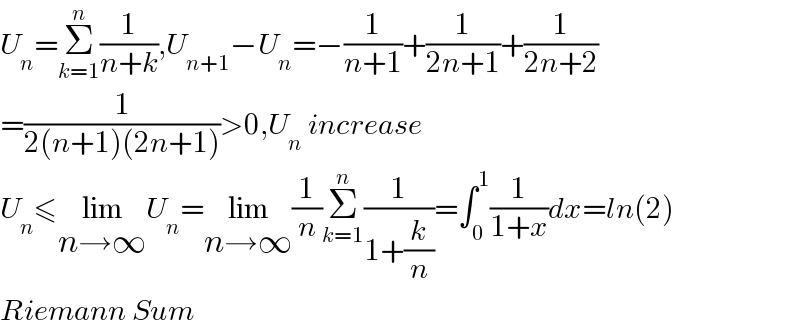
U_n =Σ_(k=1) ^n (1/(n+k)),U_(n+1) −U_n =−(1/(n+1))+(1/(2n+1))+(1/(2n+2)) =(1/(2(n+1)(2n+1)))>0,U_n increase U_n ≤lim_(n→∞) U_n =lim_(n→∞) (1/n)Σ_(k=1) ^n (1/(1+(k/n)))=∫_0 ^1 (1/(1+x))dx=ln(2) Riemann Sum
$${U}_{{n}} =\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{{n}+{k}},{U}_{{n}+\mathrm{1}} −{U}_{{n}} =−\frac{\mathrm{1}}{{n}+\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)}>\mathrm{0},{U}_{{n}} \:{increase} \\ $$$${U}_{{n}} \leqslant\underset{{n}\rightarrow\infty} {\mathrm{lim}}{U}_{{n}} =\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{{n}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{\mathrm{1}+\frac{{k}}{{n}}}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{1}+{x}}{dx}={ln}\left(\mathrm{2}\right) \\ $$$${Riemann}\:{Sum} \\ $$
Commented by aba last updated on 16/Jan/23
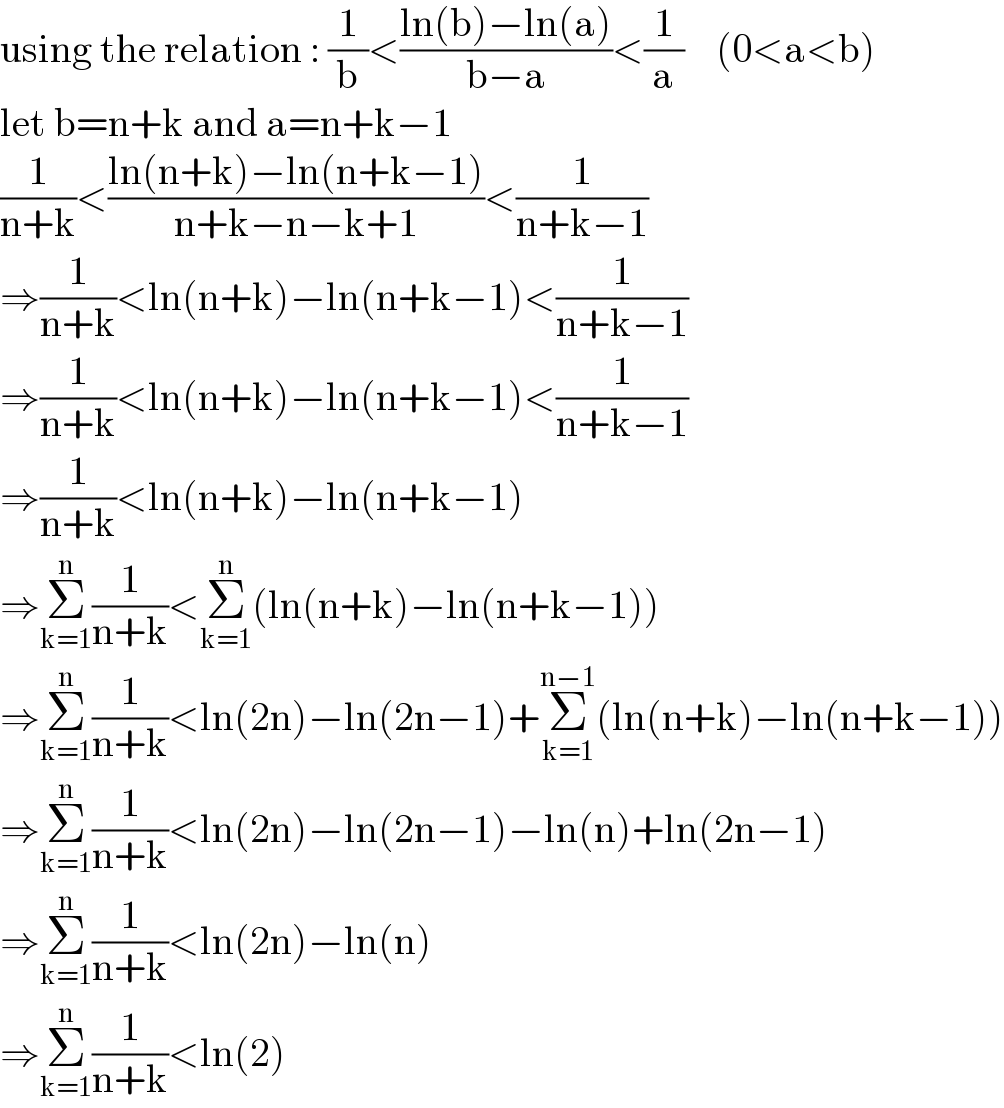
using the relation : (1/b)<((ln(b)−ln(a))/(b−a))<(1/a) (0<a<b) let b=n+k and a=n+k−1 (1/(n+k))<((ln(n+k)−ln(n+k−1))/(n+k−n−k+1))<(1/(n+k−1)) ⇒(1/(n+k))<ln(n+k)−ln(n+k−1)<(1/(n+k−1)) ⇒(1/(n+k))<ln(n+k)−ln(n+k−1)<(1/(n+k−1)) ⇒(1/(n+k))<ln(n+k)−ln(n+k−1) ⇒Σ_(k=1) ^n (1/(n+k))<Σ_(k=1) ^n (ln(n+k)−ln(n+k−1)) ⇒Σ_(k=1) ^n (1/(n+k))<ln(2n)−ln(2n−1)+Σ_(k=1) ^(n−1) (ln(n+k)−ln(n+k−1)) ⇒Σ_(k=1) ^n (1/(n+k))<ln(2n)−ln(2n−1)−ln(n)+ln(2n−1) ⇒Σ_(k=1) ^n (1/(n+k))<ln(2n)−ln(n) ⇒Σ_(k=1) ^n (1/(n+k))<ln(2)
$$\mathrm{using}\:\mathrm{the}\:\mathrm{relation}\::\:\frac{\mathrm{1}}{\mathrm{b}}<\frac{\mathrm{ln}\left(\mathrm{b}\right)−\mathrm{ln}\left(\mathrm{a}\right)}{\mathrm{b}−\mathrm{a}}<\frac{\mathrm{1}}{\mathrm{a}}\:\:\:\:\left(\mathrm{0}<\mathrm{a}<\mathrm{b}\right) \\ $$$$\mathrm{let}\:\mathrm{b}=\mathrm{n}+\mathrm{k}\:\mathrm{and}\:\mathrm{a}=\mathrm{n}+\mathrm{k}−\mathrm{1} \\ $$$$\frac{\mathrm{1}}{\mathrm{n}+\mathrm{k}}<\frac{\mathrm{ln}\left(\mathrm{n}+\mathrm{k}\right)−\mathrm{ln}\left(\mathrm{n}+\mathrm{k}−\mathrm{1}\right)}{\mathrm{n}+\mathrm{k}−\mathrm{n}−\mathrm{k}+\mathrm{1}}<\frac{\mathrm{1}}{\mathrm{n}+\mathrm{k}−\mathrm{1}} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{n}+\mathrm{k}}<\mathrm{ln}\left(\mathrm{n}+\mathrm{k}\right)−\mathrm{ln}\left(\mathrm{n}+\mathrm{k}−\mathrm{1}\right)<\frac{\mathrm{1}}{\mathrm{n}+\mathrm{k}−\mathrm{1}} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{n}+\mathrm{k}}<\mathrm{ln}\left(\mathrm{n}+\mathrm{k}\right)−\mathrm{ln}\left(\mathrm{n}+\mathrm{k}−\mathrm{1}\right)<\frac{\mathrm{1}}{\mathrm{n}+\mathrm{k}−\mathrm{1}} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{n}+\mathrm{k}}<\mathrm{ln}\left(\mathrm{n}+\mathrm{k}\right)−\mathrm{ln}\left(\mathrm{n}+\mathrm{k}−\mathrm{1}\right) \\ $$$$\Rightarrow\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\frac{\mathrm{1}}{\mathrm{n}+\mathrm{k}}<\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\left(\mathrm{ln}\left(\mathrm{n}+\mathrm{k}\right)−\mathrm{ln}\left(\mathrm{n}+\mathrm{k}−\mathrm{1}\right)\right) \\ $$$$\Rightarrow\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\frac{\mathrm{1}}{\mathrm{n}+\mathrm{k}}<\mathrm{ln}\left(\mathrm{2n}\right)−\mathrm{ln}\left(\mathrm{2n}−\mathrm{1}\right)+\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}−\mathrm{1}} {\sum}}\left(\mathrm{ln}\left(\mathrm{n}+\mathrm{k}\right)−\mathrm{ln}\left(\mathrm{n}+\mathrm{k}−\mathrm{1}\right)\right) \\ $$$$\Rightarrow\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\frac{\mathrm{1}}{\mathrm{n}+\mathrm{k}}<\mathrm{ln}\left(\mathrm{2n}\right)−\mathrm{ln}\left(\mathrm{2n}−\mathrm{1}\right)−\mathrm{ln}\left(\mathrm{n}\right)+\mathrm{ln}\left(\mathrm{2n}−\mathrm{1}\right) \\ $$$$\Rightarrow\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\frac{\mathrm{1}}{\mathrm{n}+\mathrm{k}}<\mathrm{ln}\left(\mathrm{2n}\right)−\mathrm{ln}\left(\mathrm{n}\right) \\ $$$$\Rightarrow\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\frac{\mathrm{1}}{\mathrm{n}+\mathrm{k}}<\mathrm{ln}\left(\mathrm{2}\right) \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *