Question Number 47098 by rahul 19 last updated on 04/Nov/18
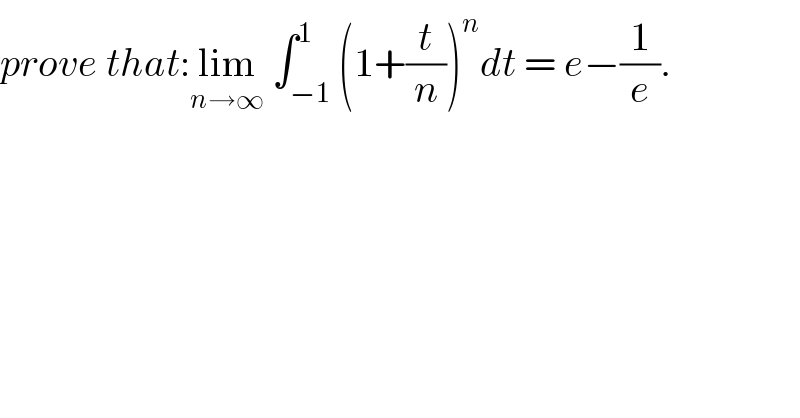
$${prove}\:{that}:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\int_{−\mathrm{1}} ^{\mathrm{1}} \left(\mathrm{1}+\frac{{t}}{{n}}\right)^{{n}} {dt}\:=\:{e}−\frac{\mathrm{1}}{{e}}. \\ $$
Commented by rahul 19 last updated on 04/Nov/18

$${My}\:{doubt}\:{is}\:{why}\:{we}\:{are}\:{taking}\:{limit} \\ $$$${first}\:{and}\:{then}\:{applying}\:{integration}?? \\ $$$${Is}\:{this}\:{correct}?? \\ $$
Commented by maxmathsup by imad last updated on 05/Nov/18

$${sir}\:{you}\:{must}\:{take}\:{a}\:{look}\:\:{and}\:{revise}\:{dominent}\:{cnvergence}\:{theorem}\:{because}\: \\ $$$${ther}\:{is}\:{a}\:{conditons}\:{to}\:{apply}\:{this}\:{theorem}\:{and}\:{its}\:{easy}\:{to}\:{use}\:{it}\:{than}\:{other} \\ $$$${method}. \\ $$
Commented by maxmathsup by imad last updated on 04/Nov/18
![let A_n = ∫_(−1) ^1 (1+(t/n))^n dt =∫_R (1+(t/n))^n χ_([−1,1]) (t)dt let f_n (t)=(1+(t/n))^n χ_([−1,1]) (t) we have lim_(n→+∞) f_n (t) =e^t χ_([−1,1]) (t) (simple convergence ) and ∣f_n (t)∣ ≤e^t ∀ t ∈[−1,1] dominent convergence give lim_(n→+∞) A_n =∫_R lim_(n→) f_n (t)dt = ∫_R e^t χ_([−1,1]) (t)dt =∫_(−1) ^1 e^t dt=[e^t ]_(−1) ^1 =e −(1/e) .](https://www.tinkutara.com/question/Q47103.png)
$${let}\:{A}_{{n}} =\:\int_{−\mathrm{1}} ^{\mathrm{1}} \left(\mathrm{1}+\frac{{t}}{{n}}\right)^{{n}} {dt}\:=\int_{{R}} \left(\mathrm{1}+\frac{{t}}{{n}}\right)^{{n}} \chi_{\left[−\mathrm{1},\mathrm{1}\right]} \left({t}\right){dt}\:{let}\:{f}_{{n}} \left({t}\right)=\left(\mathrm{1}+\frac{{t}}{{n}}\right)^{{n}} \:\chi_{\left[−\mathrm{1},\mathrm{1}\right]} \left({t}\right) \\ $$$${we}\:{have}\:{lim}_{{n}\rightarrow+\infty} {f}_{{n}} \left({t}\right)\:={e}^{{t}} \chi_{\left[−\mathrm{1},\mathrm{1}\right]} \left({t}\right)\:\left({simple}\:{convergence}\:\right)\:{and} \\ $$$$\mid{f}_{{n}} \left({t}\right)\mid\:\leqslant{e}^{{t}} \:\:\forall\:{t}\:\in\left[−\mathrm{1},\mathrm{1}\right]\:{dominent}\:{convergence}\:{give} \\ $$$${lim}_{{n}\rightarrow+\infty} {A}_{{n}} =\int_{{R}} {lim}_{{n}\rightarrow} \:{f}_{{n}} \left({t}\right){dt}\:=\:\int_{{R}} {e}^{{t}} \:\chi_{\left[−\mathrm{1},\mathrm{1}\right]} \left({t}\right){dt}\:=\int_{−\mathrm{1}} ^{\mathrm{1}} \:{e}^{{t}} {dt}=\left[{e}^{{t}} \right]_{−\mathrm{1}} ^{\mathrm{1}} \\ $$$$={e}\:−\frac{\mathrm{1}}{{e}}\:. \\ $$
Commented by maxmathsup by imad last updated on 04/Nov/18
![another method let A_n = ∫_(−1) ^1 (1+(t/n))^n dt changement (t/n)=x give A_n =∫_(−(1/n)) ^(1/n) (1+x)^n ndx =n ∫_(−(1/n)) ^(1/n) (1+x)^n dx =(n/(n+1)) [(1+x)^(n+1) ]_(−(1/n)) ^(1/n) =(n/(n+1)){(1+(1/n))^(n+1) −(1−(1/n))^(n+1) } but (1+(1/n))^(n+1) =e^((n+1)ln( 1+(1/n))) but we have ln(1+(1/n))=(1/n)+o((1/n)) ⇒ (n+1)ln(1+(1/n))=((n+1)/n) +o(1) →1 (n→+∞) also (n+1)ln(1−(1/n)) =−((n+1)/n) →−1 (n→+∞) ⇒lim_(n→+∞) A_n =lim_(n→+∞) (n/(n+1))(e−e^(−1) ) ⇒ lim_(n→+∞) A_n =e −e^(−1) .](https://www.tinkutara.com/question/Q47104.png)
$${another}\:{method}\:\:{let}\:{A}_{{n}} =\:\int_{−\mathrm{1}} ^{\mathrm{1}} \:\left(\mathrm{1}+\frac{{t}}{{n}}\right)^{{n}} \:{dt}\:\:{changement}\:\frac{{t}}{{n}}={x}\:{give} \\ $$$${A}_{{n}} =\int_{−\frac{\mathrm{1}}{{n}}} ^{\frac{\mathrm{1}}{{n}}} \:\left(\mathrm{1}+{x}\right)^{{n}} \:{ndx}\:={n}\:\int_{−\frac{\mathrm{1}}{{n}}} ^{\frac{\mathrm{1}}{{n}}} \:\left(\mathrm{1}+{x}\right)^{{n}} {dx} \\ $$$$=\frac{{n}}{{n}+\mathrm{1}}\:\left[\left(\mathrm{1}+{x}\right)^{{n}+\mathrm{1}} \right]_{−\frac{\mathrm{1}}{{n}}} ^{\frac{\mathrm{1}}{{n}}} \:=\frac{{n}}{{n}+\mathrm{1}}\left\{\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)^{{n}+\mathrm{1}} −\left(\mathrm{1}−\frac{\mathrm{1}}{{n}}\right)^{{n}+\mathrm{1}} \right\}\:{but} \\ $$$$\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)^{{n}+\mathrm{1}} \:={e}^{\left({n}+\mathrm{1}\right){ln}\left(\:\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)} \:\:{but}\:{we}\:{have}\:{ln}\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)=\frac{\mathrm{1}}{{n}}+{o}\left(\frac{\mathrm{1}}{{n}}\right)\:\Rightarrow \\ $$$$\left({n}+\mathrm{1}\right){ln}\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)=\frac{{n}+\mathrm{1}}{{n}}\:+{o}\left(\mathrm{1}\right)\:\rightarrow\mathrm{1}\:\left({n}\rightarrow+\infty\right)\:{also} \\ $$$$\left({n}+\mathrm{1}\right){ln}\left(\mathrm{1}−\frac{\mathrm{1}}{{n}}\right)\:=−\frac{{n}+\mathrm{1}}{{n}}\:\rightarrow−\mathrm{1}\:\left({n}\rightarrow+\infty\right)\:\Rightarrow{lim}_{{n}\rightarrow+\infty} {A}_{{n}} ={lim}_{{n}\rightarrow+\infty} \frac{{n}}{{n}+\mathrm{1}}\left({e}−{e}^{−\mathrm{1}} \right)\:\Rightarrow \\ $$$${lim}_{{n}\rightarrow+\infty} \:{A}_{{n}} ={e}\:−{e}^{−\mathrm{1}} \:. \\ $$$$ \\ $$
Commented by peter frank last updated on 04/Nov/18

$$\mathrm{pls}\:\mathrm{help}\:\mathrm{QN}\:\mathrm{46827} \\ $$
Commented by rahul 19 last updated on 05/Nov/18

$${Prof}\:{Abdo}, \\ $$$${pls}\:{clear}\:{my}\:{doubt}: \\ $$$${In}\:{this}\:{problem}\:{we}\:{are}\:{first}\:{given}\:{to} \\ $$$${integrate}\:{and}\:{then}\:{to}\:{apply}\:{limits}… \\ $$$${But}\:{if}\:{we}\:{first}\:{apply}\:{limits}\:{and}\:{then} \\ $$$${integrate}\:{we}\:{are}\:{getting}\:{same}\:{result} \\ $$$${and}\:{which}\:{is}\:{shorter}\:{method}\:{too}! \\ $$$${So},\:{is}\:{this}\:{method}\:{correct}\:{or}\:{is}\:{it}\:{just}\:{a}\: \\ $$$${coincidence}? \\ $$
Commented by rahul 19 last updated on 05/Nov/18

$${okay}\:{thank}\:{you}\:{prof}\:! \\ $$$${I}'{m}\:{new}\:{to}\:{dominent}\:{convergence}\:!! \\ $$
Commented by maxmathsup by imad last updated on 06/Nov/18
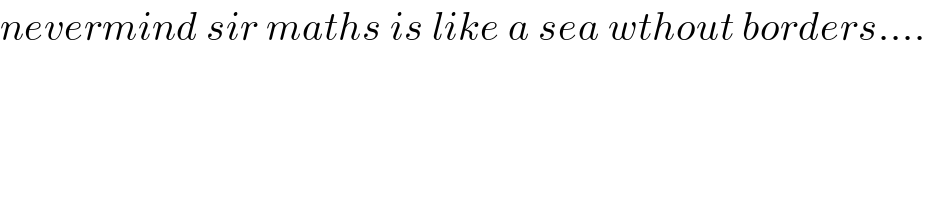
$${nevermind}\:{sir}\:{maths}\:{is}\:{like}\:{a}\:{sea}\:{wthout}\:{borders}…. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 04/Nov/18
![I=∫(1+(t/n))^n dt k=1+(t/n) dk=(dt/n) ∫k^n ×ndk n×(k^(n+1) /(n+1))+c_1 so the intregsl is (n/(n+1))×∣(1+(t/n))^(n+1) ∣_(−1) ^1 (n/(n+1))[(1+(1/n))^(n+1) −(1−(1/n))^(n+1) now apply limit lim_(n→∞) (1/(1+(1/n)))[(1+(1/n))^(n+1) −(1−(1/n))^(n+1) ] =lim_(n→∞) (1/(1+(1/n)))×[lim_(n→∞) (1+(1/n))×lim_(n→∞) (1+(1/n))^n −lim_(n→∞[) (1−(1/n))×lim_(n→∞) (1−(1/n))^n ] =(1/(1+0))×[(1+0)×e−(1−0)×e^(−1) ] =(e−(1/e)) first intregation then limit done pls check... now formula lip_(n→∞) =lil_(n→∞) ×li_(n→∞) nz=li_(n→∞) =li_(y→0) z=e li_(n→∞) lnp=li_(n→∞) w=(1/n) li_(w→0) =li_(w→0)](https://www.tinkutara.com/question/Q47100.png)
$${I}=\int\left(\mathrm{1}+\frac{{t}}{{n}}\right)^{{n}} {dt} \\ $$$${k}=\mathrm{1}+\frac{{t}}{{n}}\:\:\:{dk}=\frac{{dt}}{{n}} \\ $$$$\int{k}^{{n}} ×{ndk} \\ $$$${n}×\frac{{k}^{{n}+\mathrm{1}} }{{n}+\mathrm{1}}+{c}_{\mathrm{1}} \\ $$$${so}\:{the}\:{intregsl}\:{is} \\ $$$$\frac{{n}}{{n}+\mathrm{1}}×\mid\left(\mathrm{1}+\frac{{t}}{{n}}\right)^{{n}+\mathrm{1}} \mid_{−\mathrm{1}} ^{\mathrm{1}} \\ $$$$\frac{{n}}{{n}+\mathrm{1}}\left[\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)^{{n}+\mathrm{1}} −\left(\mathrm{1}−\frac{\mathrm{1}}{{n}}\right)^{{n}+\mathrm{1}} \right. \\ $$$${now}\:{apply}\:{limit} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{1}}{{n}}}\left[\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)^{{n}+\mathrm{1}} −\left(\mathrm{1}−\frac{\mathrm{1}}{{n}}\right)^{{n}+\mathrm{1}} \right] \\ $$$$=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{1}}{{n}}}×\left[\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)×\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)^{{n}} −\underset{{n}\rightarrow\infty\left[\right.} {\mathrm{lim}}\left(\mathrm{1}−\frac{\mathrm{1}}{{n}}\right)×\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left(\mathrm{1}−\frac{\mathrm{1}}{{n}}\right)^{{n}} \right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{1}+\mathrm{0}}×\left[\left(\mathrm{1}+\mathrm{0}\right)×{e}−\left(\mathrm{1}−\mathrm{0}\right)×{e}^{−\mathrm{1}} \right] \\ $$$$=\left({e}−\frac{\mathrm{1}}{{e}}\right) \\ $$$${first}\:{intregation}\:{then}\:{limit}\:{done} \\ $$$${pls}\:{check}… \\ $$$${now}\:{formula} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{li}{p}} \\ $$$$=\underset{{n}\rightarrow\infty} {\mathrm{li}{l}}×\underset{{n}\rightarrow\infty} {\mathrm{li}} \\ $$$${nz}=\underset{{n}\rightarrow\infty} {\mathrm{li}} \\ $$$$=\underset{{y}\rightarrow\mathrm{0}} {\mathrm{li}} \\ $$$${z}={e} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{li}} \\ $$$${lnp}=\underset{{n}\rightarrow\infty} {\mathrm{li}} \\ $$$${w}=\frac{\mathrm{1}}{{n}}\:\:\:\:\:\:\:\:\:\underset{{w}\rightarrow\mathrm{0}} {\mathrm{li}} \\ $$$$=\underset{{w}\rightarrow\mathrm{0}} {\mathrm{li}} \\ $$
Commented by rahul 19 last updated on 05/Nov/18
thanks sir ����
