Menu Close

prove-that-lim-x-n-2-1-cos-1-n-1-cos-1-n-1-cos-1-n-1-2-

Tinku Tara 0 Comments
Pin




Question Number 82160 by M±th+et£s last updated on 18/Feb/20
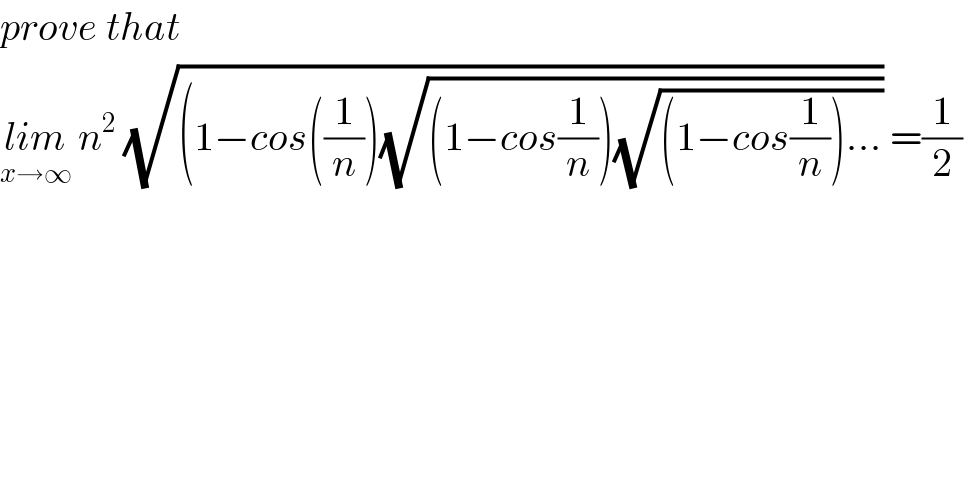
prove that lim_(x→∞) n^2 (√((1−cos((1/n))(√((1−cos(1/n))(√((1−cos(1/n))...)))))) =(1/2)
$${prove}\:{that} \\ $$$$\underset{{x}\rightarrow\infty} {{lim}}\:{n}^{\mathrm{2}} \:\sqrt{\left(\mathrm{1}−{cos}\left(\frac{\mathrm{1}}{{n}}\right)\sqrt{\left(\mathrm{1}−{cos}\frac{\mathrm{1}}{{n}}\right)\sqrt{\left(\mathrm{1}−{cos}\frac{\mathrm{1}}{{n}}\right)…}}\right.}\:=\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Answered by MJS last updated on 18/Feb/20
w=(√((1−cos (1/n))(√((1−cos (1/n))(√(...)))))) w^2 =(1−cos (1/n))w ⇒ w=0∨w=1−cos (1/n) ...=lim_(n→∞) n^2 (1−cos (1/n)) let n=(1/k) lim_(k→0) ((1−cos k)/k^2 ) =lim_(k→0) (((d^2 /dk^2 )[1−cos k])/((d^2 /dk^2 )[k^2 ])) = =lim_(k→0) ((cos k)/2) =(1/2)
$${w}=\sqrt{\left(\mathrm{1}−\mathrm{cos}\:\frac{\mathrm{1}}{{n}}\right)\sqrt{\left(\mathrm{1}−\mathrm{cos}\:\frac{\mathrm{1}}{{n}}\right)\sqrt{…}}} \\ $$$${w}^{\mathrm{2}} =\left(\mathrm{1}−\mathrm{cos}\:\frac{\mathrm{1}}{{n}}\right){w}\:\Rightarrow\:{w}=\mathrm{0}\vee{w}=\mathrm{1}−\mathrm{cos}\:\frac{\mathrm{1}}{{n}} \\ $$$$…=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:{n}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{cos}\:\frac{\mathrm{1}}{{n}}\right) \\ $$$$\mathrm{let}\:{n}=\frac{\mathrm{1}}{{k}} \\ $$$$\underset{{k}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}−\mathrm{cos}\:{k}}{{k}^{\mathrm{2}} }\:=\underset{{k}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\frac{{d}^{\mathrm{2}} }{{dk}^{\mathrm{2}} }\left[\mathrm{1}−\mathrm{cos}\:{k}\right]}{\frac{{d}^{\mathrm{2}} }{{dk}^{\mathrm{2}} }\left[{k}^{\mathrm{2}} \right]}\:= \\ $$$$=\underset{{k}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{cos}\:{k}}{\mathrm{2}}\:=\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Answered by mr W last updated on 18/Feb/20
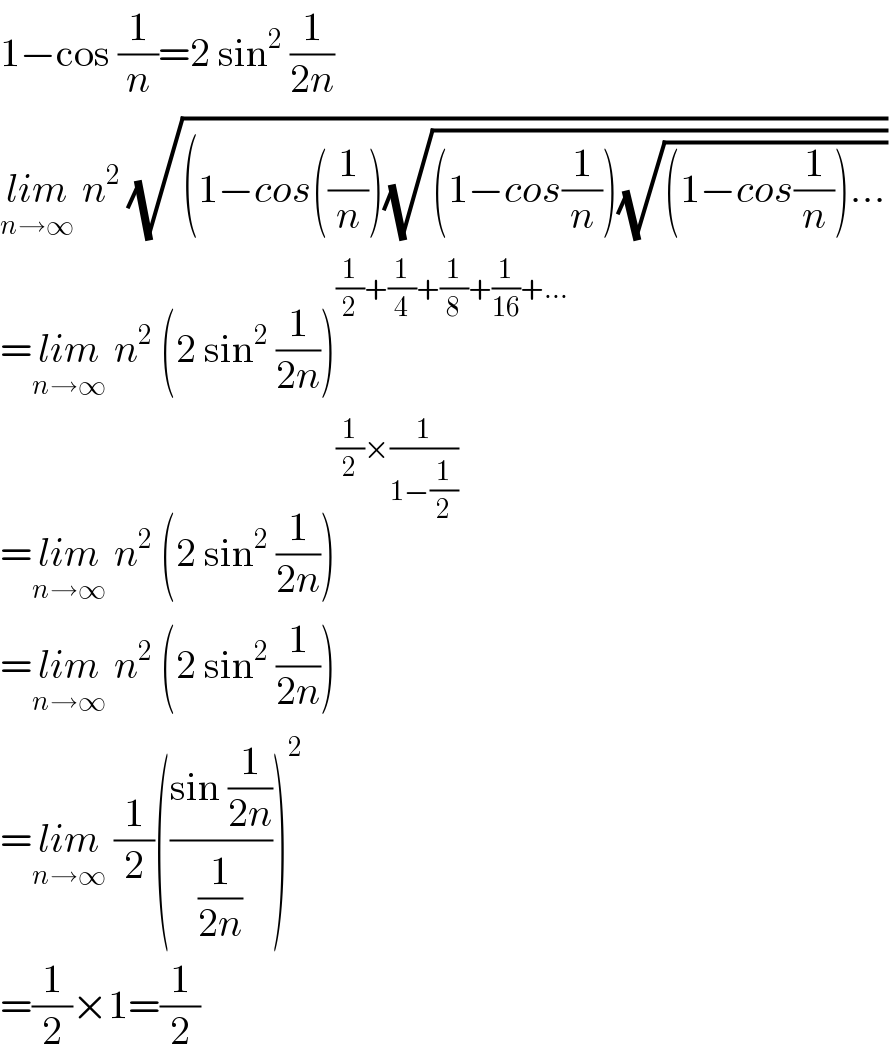
1−cos (1/n)=2 sin^2 (1/(2n)) lim_(n→∞) n^2 (√((1−cos((1/n))(√((1−cos(1/n))(√((1−cos(1/n))...)))))) =lim_(n→∞) n^2 (2 sin^2 (1/(2n)))^((1/2)+(1/4)+(1/8)+(1/(16))+...) =lim_(n→∞) n^2 (2 sin^2 (1/(2n)))^((1/2)×(1/(1−(1/2)))) =lim_(n→∞) n^2 (2 sin^2 (1/(2n))) =lim_(n→∞) (1/2)(((sin (1/(2n)))/(1/(2n))))^2 =(1/2)×1=(1/2)
$$\mathrm{1}−\mathrm{cos}\:\frac{\mathrm{1}}{{n}}=\mathrm{2}\:\mathrm{sin}^{\mathrm{2}} \:\frac{\mathrm{1}}{\mathrm{2}{n}} \\ $$$$\underset{{n}\rightarrow\infty} {{lim}}\:{n}^{\mathrm{2}} \:\sqrt{\left(\mathrm{1}−{cos}\left(\frac{\mathrm{1}}{{n}}\right)\sqrt{\left(\mathrm{1}−{cos}\frac{\mathrm{1}}{{n}}\right)\sqrt{\left(\mathrm{1}−{cos}\frac{\mathrm{1}}{{n}}\right)…}}\right.}\: \\ $$$$=\underset{{n}\rightarrow\infty} {{lim}}\:{n}^{\mathrm{2}} \:\left(\mathrm{2}\:\mathrm{sin}^{\mathrm{2}} \:\frac{\mathrm{1}}{\mathrm{2}{n}}\right)^{\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{8}}+\frac{\mathrm{1}}{\mathrm{16}}+…} \\ $$$$=\underset{{n}\rightarrow\infty} {{lim}}\:{n}^{\mathrm{2}} \:\left(\mathrm{2}\:\mathrm{sin}^{\mathrm{2}} \:\frac{\mathrm{1}}{\mathrm{2}{n}}\right)^{\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}}} \\ $$$$=\underset{{n}\rightarrow\infty} {{lim}}\:{n}^{\mathrm{2}} \:\left(\mathrm{2}\:\mathrm{sin}^{\mathrm{2}} \:\frac{\mathrm{1}}{\mathrm{2}{n}}\right) \\ $$$$=\underset{{n}\rightarrow\infty} {{lim}}\:\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{sin}\:\frac{\mathrm{1}}{\mathrm{2}{n}}}{\frac{\mathrm{1}}{\mathrm{2}{n}}}\right)^{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{1}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *