Question Number 96729 by qwertasdf last updated on 04/Jun/20
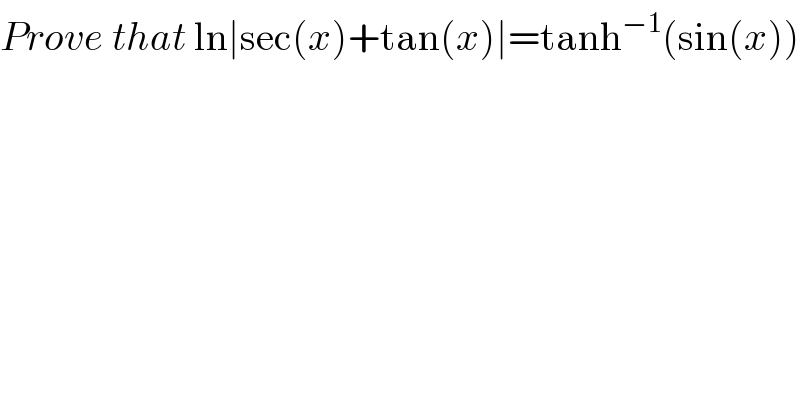
$${Prove}\:{that}\:\mathrm{ln}\mid\mathrm{sec}\left({x}\right)+\mathrm{tan}\left({x}\right)\mid=\mathrm{tanh}^{−\mathrm{1}} \left(\mathrm{sin}\left({x}\right)\right) \\ $$
Commented by prakash jain last updated on 04/Jun/20

$$\mathrm{tanh}^{−\mathrm{1}} \left({x}\right)=\mathrm{ln}\:\left(\frac{\mathrm{1}+{x}}{\mathrm{1}−{x}}\right)^{\mathrm{1}/\mathrm{2}} \\ $$$$\mathrm{tanh}^{−\mathrm{1}} \left(\mathrm{sin}\:\left({x}\right)\right)=\mathrm{ln}\:\frac{\mathrm{1}+\mathrm{sin}\:{x}}{\mathrm{1}−\mathrm{sin}\:{x}} \\ $$$$\mathrm{When}\:\mathrm{sin}\:{x}\neq\mathrm{1} \\ $$$$\mathrm{ln}\left(\:\frac{\mathrm{1}+\mathrm{sin}\:{x}}{\mathrm{1}−\mathrm{sin}\:{x}}×\frac{\mathrm{1}+\mathrm{sin}\:{x}}{\mathrm{1}+\mathrm{sin}\:{x}}\right)^{\mathrm{1}/\mathrm{2}} \\ $$$$\mathrm{ln}\:\left(\frac{\mathrm{1}+\mathrm{2sin}\:{x}+\mathrm{sin}^{\mathrm{2}} {x}}{\mathrm{1}−\mathrm{sin}^{\mathrm{2}} {x}}\right)^{\mathrm{1}/\mathrm{2}} \\ $$$$=\mathrm{ln}\:\left(\frac{\mathrm{1}}{\mathrm{cos}^{\mathrm{2}} {x}}+\mathrm{2tan}\:{x}\mathrm{sec}\:{x}+\mathrm{tan}^{\mathrm{2}} {x}\right)^{\mathrm{1}/\mathrm{2}} \\ $$$$=\mathrm{ln}\:\left(\left(\mathrm{sec}\:{x}+\mathrm{tan}\:{x}\right)^{\mathrm{2}} \right)^{\mathrm{1}/\mathrm{2}} \\ $$$$=\mathrm{ln}\:\mid\mathrm{sec}\:{x}+\mathrm{tan}\:{x}\mid \\ $$$$\mathrm{equality}\:\mathrm{only}\:\mathrm{valid}\:\mathrm{when}\:\mathrm{sin}\:{x}\neq\mathrm{1} \\ $$
Answered by Ar Brandon last updated on 04/Jun/20
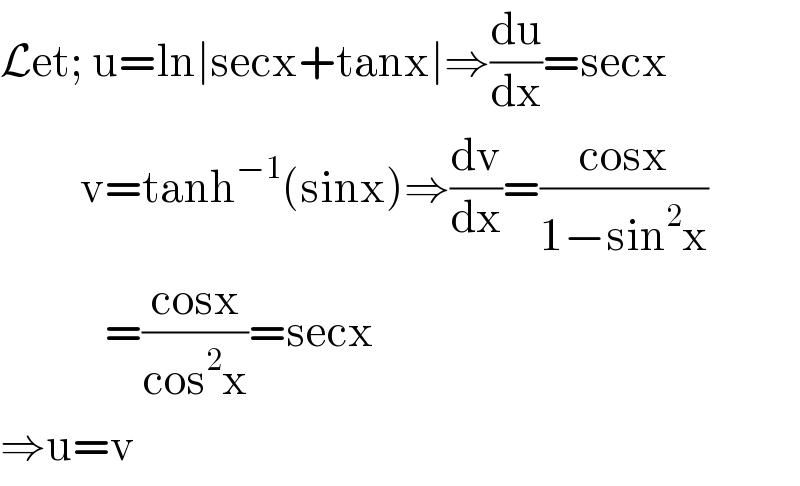
$$\mathcal{L}\mathrm{et};\:\mathrm{u}=\mathrm{ln}\mid\mathrm{secx}+\mathrm{tanx}\mid\Rightarrow\frac{\mathrm{du}}{\mathrm{dx}}=\mathrm{secx} \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathrm{v}=\mathrm{tanh}^{−\mathrm{1}} \left(\mathrm{sinx}\right)\Rightarrow\frac{\mathrm{dv}}{\mathrm{dx}}=\frac{\mathrm{cosx}}{\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \mathrm{x}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{cosx}}{\mathrm{cos}^{\mathrm{2}} \mathrm{x}}=\mathrm{secx} \\ $$$$\Rightarrow\mathrm{u}=\mathrm{v} \\ $$
Commented by Ar Brandon last updated on 04/Jun/20

$$\mathrm{But}\:\mathrm{in}\:\mathrm{this}\:\mathrm{case}\:\mathrm{the}\:\mathrm{constants}\:\mathrm{are}\:\mathrm{all}\:\mathrm{0} \\ $$$$\mathcal{I}\:\mathrm{feel}\:\mathrm{that}\:\mathrm{makes}\:\mathrm{a}\:\mathrm{difference}.\:\mathrm{What}\:\mathrm{do} \\ $$$$\mathrm{you}\:\mathrm{think}\:\mathrm{Sir}? \\ $$
Commented by prakash jain last updated on 04/Jun/20

$$\frac{{du}}{{dx}}=\frac{{dv}}{{dx}}\nRightarrow{u}={v} \\ $$$${ex}: \\ $$$${u}={x}^{\mathrm{2}} +{c} \\ $$$${v}={x}^{\mathrm{2}} \\ $$
Commented by prakash jain last updated on 04/Jun/20

$$\mathrm{But}\:\mathrm{then}\:\mathrm{you}\:\mathrm{will}\:\mathrm{need}\:\mathrm{a}\:\mathrm{formal} \\ $$$$\mathrm{proof}\:\mathrm{that}\:\mathrm{there}\:\mathrm{is}\:\mathrm{no}\:\mathrm{constant}\:\mathrm{term}. \\ $$$$\mathrm{For}\:\mathrm{example}\:\mathrm{function}\:\mathrm{like}\:\mathrm{cos}{x},{e}^{{x}} \\ $$$$\mathrm{have}\:\mathrm{terms}\:\mathrm{independent}\:\mathrm{of}\:{x}. \\ $$
Commented by prakash jain last updated on 04/Jun/20

$$\mathrm{Also}\:\left(\mathrm{sec}\left({x}\right)+\mathrm{tan}\:\left({x}\right)\right)\:\mathrm{has}\:\mathrm{terms} \\ $$$$\mathrm{independent}\:\mathrm{of}\:{x}.\: \\ $$$$\mathrm{ln}\mid\mathrm{sec}\:{x}+\mathrm{tan}\:{x}\mid\:\:\mathrm{does}\:\mathrm{not}\:\mathrm{have} \\ $$$$\mathrm{terms}\:\mathrm{independent}\:\mathrm{of}\:{x}. \\ $$
Commented by Ar Brandon last updated on 04/Jun/20

$$\mathrm{OK}\:\mathrm{thanks}\:\mathrm{Sir}\:\mathrm{for}\:\mathrm{your}\:\mathrm{opinion}.\:\mathrm{I}\:\mathrm{tried}\:\mathrm{a}\:\mathrm{different} \\ $$$$\mathrm{approach}. \\ $$
Commented by 1549442205 last updated on 05/Jun/20

$$\mathrm{Clearly},\mathrm{by}\:\mathrm{your}\:\mathrm{argument}\:\mathrm{it}\:\mathrm{follows}\:\mathrm{that}\:\mathrm{the}\:\mathrm{equality} \\ $$$$\frac{\mathrm{du}}{\mathrm{dx}}=\frac{\mathrm{dv}}{\mathrm{dx}}\:\mathrm{is}\:\mathrm{simple}\:\mathrm{a}\:\mathrm{need}\:\mathrm{condition}\:\mathrm{to}\:\mathrm{u}=\mathrm{v}\:\mathrm{but} \\ $$$$\mathrm{it}\:\mathrm{isn}'\mathrm{t}\:\mathrm{a}\:\mathrm{enough}\:\mathrm{condition}\:\mathrm{to}\:\mathrm{u}=\mathrm{v} \\ $$
Answered by Ar Brandon last updated on 04/Jun/20
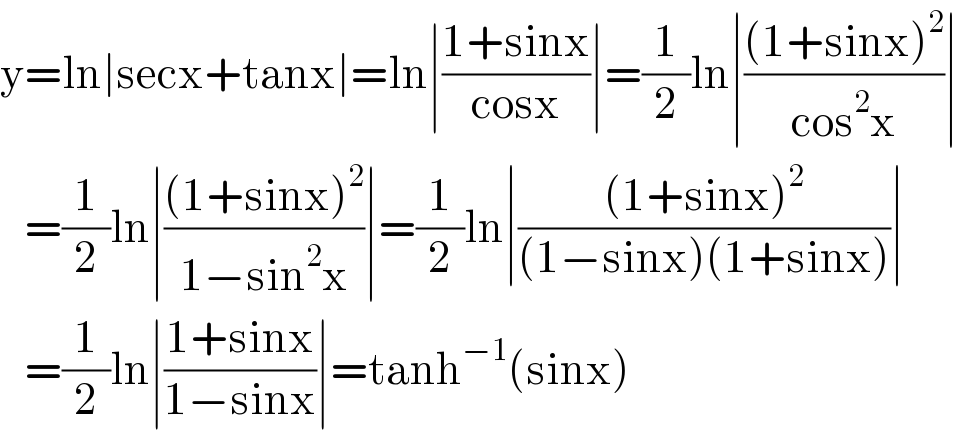
$$\mathrm{y}=\mathrm{ln}\mid\mathrm{secx}+\mathrm{tanx}\mid=\mathrm{ln}\mid\frac{\mathrm{1}+\mathrm{sinx}}{\mathrm{cosx}}\mid=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\mid\frac{\left(\mathrm{1}+\mathrm{sinx}\right)^{\mathrm{2}} }{\mathrm{cos}^{\mathrm{2}} \mathrm{x}}\mid \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\mid\frac{\left(\mathrm{1}+\mathrm{sinx}\right)^{\mathrm{2}} }{\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \mathrm{x}}\mid=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\mid\frac{\left(\mathrm{1}+\mathrm{sinx}\right)^{\mathrm{2}} }{\left(\mathrm{1}−\mathrm{sinx}\right)\left(\mathrm{1}+\mathrm{sinx}\right)}\mid \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\mid\frac{\mathrm{1}+\mathrm{sinx}}{\mathrm{1}−\mathrm{sinx}}\mid=\mathrm{tanh}^{−\mathrm{1}} \left(\mathrm{sinx}\right) \\ $$
