prove-that-ln-x-is-irrational-for-x-natural-

Question Number 40434 by vitlu last updated on 21/Jul/18

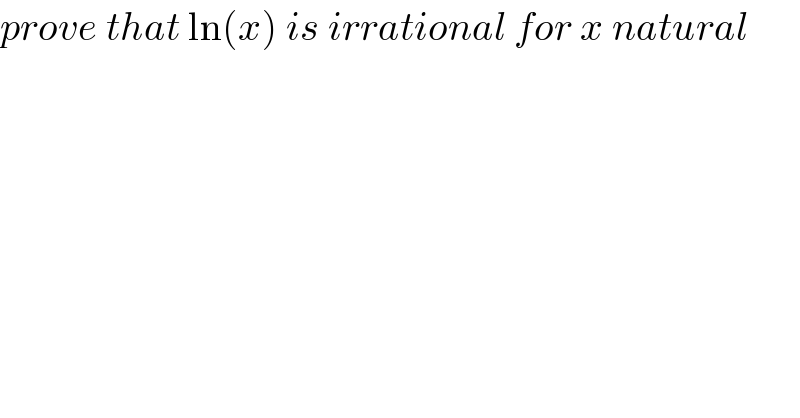
p r o v e t h a t \ln (x) i s i r r a t i o n a l f o r x n a t u r a l

Commented by math khazana by abdo last updated on 21/Jul/18

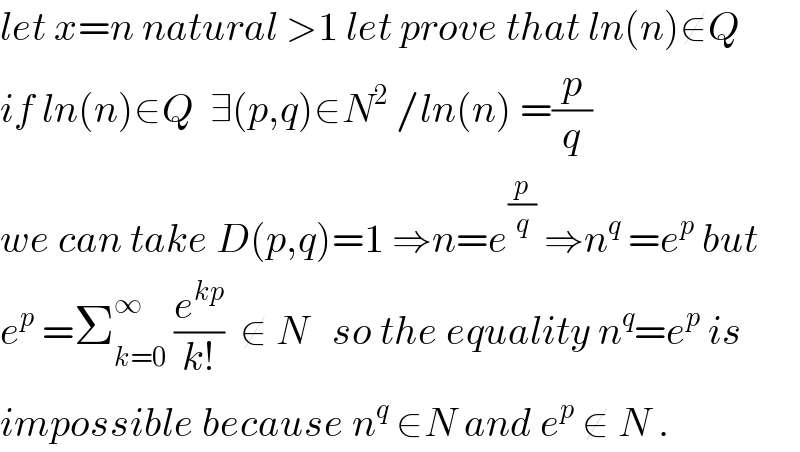
l e t x = n n a t u r a l > 1 l e t p r o v e t h a t l n (n) \notin Q

i f l n (n) \in Q \exists (p, q) \in N^{2} / l n (n) = \frac{p}{q}

w e c a n t a k e D (p, q) = 1 \Rightarrow n = e^{\frac{p}{q}} \Rightarrow n^{q} = e^{p} b u t

e^{p} = \sum_{k = 0}^{\infty} \frac{e^{k p}}{k!} \notin N s o t h e e q u a l i t y n^{q} = e^{p} i s

i m p o s s i b l e b e c a u s e n^{q} \in N a n d e^{p} \notin N .

Commented by vitlu last updated on 21/Jul/18

t h a n k s

Commented by maxmathsup by imad last updated on 21/Jul/18

y o u a r e w e c o m e