Question Number 166110 by naka3546 last updated on 13/Feb/22
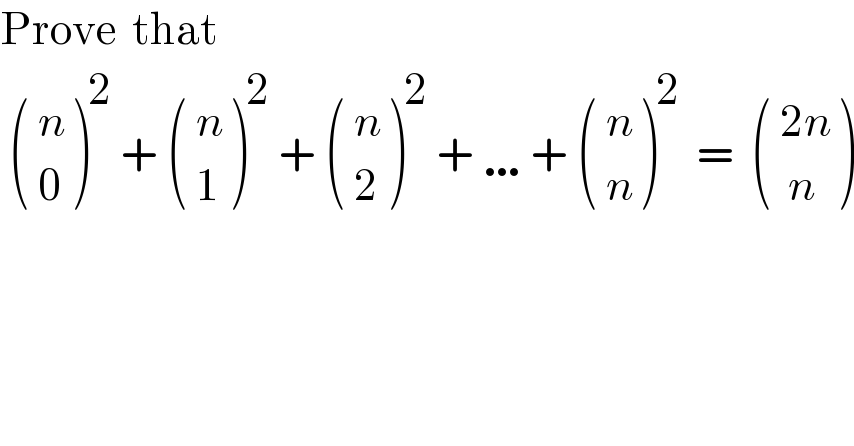
$$\mathrm{Prove}\:\:\mathrm{that} \\ $$$$\:\begin{pmatrix}{\:{n}}\\{\:\mathrm{0}}\end{pmatrix}^{\mathrm{2}} \:+\:\begin{pmatrix}{\:{n}}\\{\:\mathrm{1}}\end{pmatrix}^{\mathrm{2}} \:+\:\begin{pmatrix}{\:{n}}\\{\:\mathrm{2}}\end{pmatrix}^{\mathrm{2}} \:+\:\ldots+\:\begin{pmatrix}{\:{n}}\\{\:{n}}\end{pmatrix}^{\mathrm{2}} \:\:=\:\:\begin{pmatrix}{\:\mathrm{2}{n}}\\{\:\:{n}}\end{pmatrix} \\ $$
Answered by qaz last updated on 13/Feb/22
^n Σ_(k=0) ^n ((n),(k) )z^k =[z^n ](1+z)^(2n) = (((2n)),(n) )](https://www.tinkutara.com/question/Q166115.png)
$$\begin{pmatrix}{\mathrm{n}}\\{\mathrm{0}}\end{pmatrix}^{\mathrm{2}} +\begin{pmatrix}{\mathrm{n}}\\{\mathrm{1}}\end{pmatrix}^{\mathrm{2}} +…+\begin{pmatrix}{\mathrm{n}}\\{\mathrm{n}}\end{pmatrix}^{\mathrm{2}} \\ $$$$=\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{n}} {\sum}}\begin{pmatrix}{\mathrm{n}}\\{\mathrm{k}}\end{pmatrix}^{\mathrm{2}} \\ $$$$=\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{n}} {\sum}}\begin{pmatrix}{\mathrm{n}}\\{\mathrm{k}}\end{pmatrix}\begin{pmatrix}{\mathrm{n}}\\{\mathrm{n}−\mathrm{k}}\end{pmatrix} \\ $$$$=\left[\mathrm{z}^{\mathrm{n}} \right]\left(\mathrm{1}+\mathrm{z}\right)^{\mathrm{n}} \underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{n}} {\sum}}\begin{pmatrix}{\mathrm{n}}\\{\mathrm{k}}\end{pmatrix}\mathrm{z}^{\mathrm{k}} \\ $$$$=\left[\mathrm{z}^{\mathrm{n}} \right]\left(\mathrm{1}+\mathrm{z}\right)^{\mathrm{2n}} \\ $$$$=\begin{pmatrix}{\mathrm{2n}}\\{\mathrm{n}}\end{pmatrix} \\ $$
Commented by naka3546 last updated on 13/Feb/22

$$\mathrm{thank}\:\mathrm{you}\:,\:\mathrm{sir}. \\ $$
