Question Number 20091 by Tinkutara last updated on 21/Aug/17
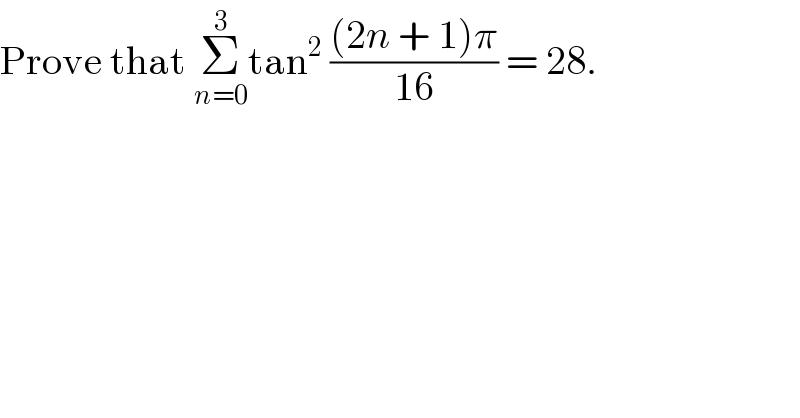
$$\mathrm{Prove}\:\mathrm{that}\:\underset{{n}=\mathrm{0}} {\overset{\mathrm{3}} {\sum}}\mathrm{tan}^{\mathrm{2}} \:\frac{\left(\mathrm{2}{n}\:+\:\mathrm{1}\right)\pi}{\mathrm{16}}\:=\:\mathrm{28}. \\ $$
Answered by ajfour last updated on 21/Aug/17
![((sin^2 A)/(cos^2 A))+((sin^2 B)/(cos^2 B))=((sin^2 Acos^2 B+cos^2 Asin^2 B)/(cos^2 Acos^2 B)) =(([sin (A+B)+sin (A−B)]^2 +[sin (A+B)−sin (A−B)]^2 )/([cos (A+B)+cos (A−B)]^2 )) =((2[sin^2 (A+B)+sin^2 (A−B)])/([cos (A+B)+cos (A−B)]^2 )) For A=(π/(16)) , B=((7π)/(16)) ; C=((3π)/(16)) , D=((5π)/(16)) sin (A+B)= sin (C+D)=1 ; cos (A+B)= cos (C+D)= 0 , hence Σtan^2 (((2n+1)π)/(16)) = ((2[1+sin^2 ((3π)/8)])/(cos^2 ((3π)/8))) + ((2[1+sin^2 (π/8)])/(cos^2 (π/8))) = ((4+4sin^2 ((3π)/8))/(2cos^2 ((3π)/8))) + ((4+4sin^2 (π/8))/(2cos^2 (π/8))) =((4+2−2cos ((3π)/4))/(1+cos ((3π)/4))) + ((4+2−2cos (π/4))/(1+cos (π/4))) =((6+(√2))/((1−(1/( (√2)))))) + ((6−(√2))/((1+(1/( (√2)))))) =((6(√2)+2)/( (√2)−1))+((6(√2)−2)/( (√2)+1)) =(12+6(√2)+2(√2)+2)+(12−6(√2)−2(√2)+2) = 28 .](https://www.tinkutara.com/question/Q20096.png)
$$\frac{\mathrm{sin}\:^{\mathrm{2}} {A}}{\mathrm{cos}\:^{\mathrm{2}} {A}}+\frac{\mathrm{sin}\:^{\mathrm{2}} {B}}{\mathrm{cos}\:^{\mathrm{2}} {B}}=\frac{\mathrm{sin}\:^{\mathrm{2}} {A}\mathrm{cos}\:^{\mathrm{2}} {B}+\mathrm{cos}\:^{\mathrm{2}} {A}\mathrm{sin}\:^{\mathrm{2}} {B}}{\mathrm{cos}\:^{\mathrm{2}} {A}\mathrm{cos}\:^{\mathrm{2}} {B}} \\ $$$$=\frac{\left[\mathrm{sin}\:\left({A}+{B}\right)+\mathrm{sin}\:\left({A}−{B}\right)\right]^{\mathrm{2}} +\left[\mathrm{sin}\:\left({A}+{B}\right)−\mathrm{sin}\:\left({A}−{B}\right)\right]^{\mathrm{2}} }{\left[\mathrm{cos}\:\left({A}+{B}\right)+\mathrm{cos}\:\left({A}−{B}\right)\right]^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{2}\left[\mathrm{sin}\:^{\mathrm{2}} \left({A}+{B}\right)+\mathrm{sin}\:^{\mathrm{2}} \left({A}−{B}\right)\right]}{\left[\mathrm{cos}\:\left({A}+{B}\right)+\mathrm{cos}\:\left({A}−{B}\right)\right]^{\mathrm{2}} } \\ $$$${For}\:{A}=\frac{\pi}{\mathrm{16}}\:\:,\:{B}=\frac{\mathrm{7}\pi}{\mathrm{16}}\:\:\:;\:\:\:{C}=\frac{\mathrm{3}\pi}{\mathrm{16}}\:,\:{D}=\frac{\mathrm{5}\pi}{\mathrm{16}} \\ $$$$\mathrm{sin}\:\left({A}+{B}\right)=\:\mathrm{sin}\:\left({C}+{D}\right)=\mathrm{1}\:\:\:;\: \\ $$$$\mathrm{cos}\:\left({A}+{B}\right)=\:\mathrm{cos}\:\left({C}+{D}\right)=\:\mathrm{0}\:,\:{hence} \\ $$$$\Sigma\mathrm{tan}\:^{\mathrm{2}} \frac{\left(\mathrm{2}{n}+\mathrm{1}\right)\pi}{\mathrm{16}}\:=\: \\ $$$$\:\:\:\:\frac{\mathrm{2}\left[\mathrm{1}+\mathrm{sin}\:^{\mathrm{2}} \:\frac{\mathrm{3}\pi}{\mathrm{8}}\right]}{\mathrm{cos}\:^{\mathrm{2}} \:\frac{\mathrm{3}\pi}{\mathrm{8}}}\:+\:\frac{\mathrm{2}\left[\mathrm{1}+\mathrm{sin}\:^{\mathrm{2}} \frac{\pi}{\mathrm{8}}\right]}{\mathrm{cos}\:^{\mathrm{2}} \frac{\pi}{\mathrm{8}}} \\ $$$$\:\:=\:\frac{\mathrm{4}+\mathrm{4sin}\:^{\mathrm{2}} \frac{\mathrm{3}\pi}{\mathrm{8}}}{\mathrm{2cos}\:^{\mathrm{2}} \:\frac{\mathrm{3}\pi}{\mathrm{8}}}\:+\:\frac{\mathrm{4}+\mathrm{4sin}\:^{\mathrm{2}} \frac{\pi}{\mathrm{8}}}{\mathrm{2cos}\:^{\mathrm{2}} \frac{\pi}{\mathrm{8}}} \\ $$$$\:\:=\frac{\mathrm{4}+\mathrm{2}−\mathrm{2cos}\:\frac{\mathrm{3}\pi}{\mathrm{4}}}{\mathrm{1}+\mathrm{cos}\:\frac{\mathrm{3}\pi}{\mathrm{4}}}\:+\:\frac{\mathrm{4}+\mathrm{2}−\mathrm{2cos}\:\frac{\pi}{\mathrm{4}}}{\mathrm{1}+\mathrm{cos}\:\frac{\pi}{\mathrm{4}}} \\ $$$$\:\:=\frac{\mathrm{6}+\sqrt{\mathrm{2}}}{\left(\mathrm{1}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)}\:+\:\frac{\mathrm{6}−\sqrt{\mathrm{2}}}{\left(\mathrm{1}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)}\:=\frac{\mathrm{6}\sqrt{\mathrm{2}}+\mathrm{2}}{\:\sqrt{\mathrm{2}}−\mathrm{1}}+\frac{\mathrm{6}\sqrt{\mathrm{2}}−\mathrm{2}}{\:\sqrt{\mathrm{2}}+\mathrm{1}} \\ $$$$\:\:=\left(\mathrm{12}+\mathrm{6}\sqrt{\mathrm{2}}+\mathrm{2}\sqrt{\mathrm{2}}+\mathrm{2}\right)+\left(\mathrm{12}−\mathrm{6}\sqrt{\mathrm{2}}−\mathrm{2}\sqrt{\mathrm{2}}+\mathrm{2}\right) \\ $$$$\:=\:\mathrm{28}\:. \\ $$
Commented by Tinkutara last updated on 21/Aug/17
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}! \\ $$
