Question Number 90562 by Tony Lin last updated on 24/Apr/20
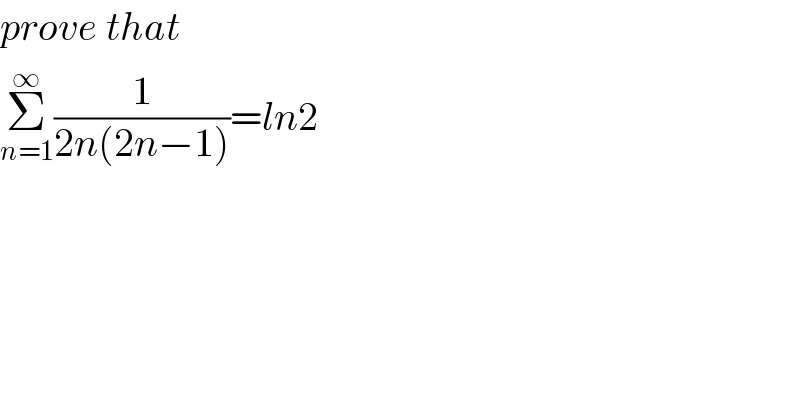
$${prove}\:{that} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{2}{n}\left(\mathrm{2}{n}−\mathrm{1}\right)}={ln}\mathrm{2} \\ $$
Commented by mathmax by abdo last updated on 24/Apr/20
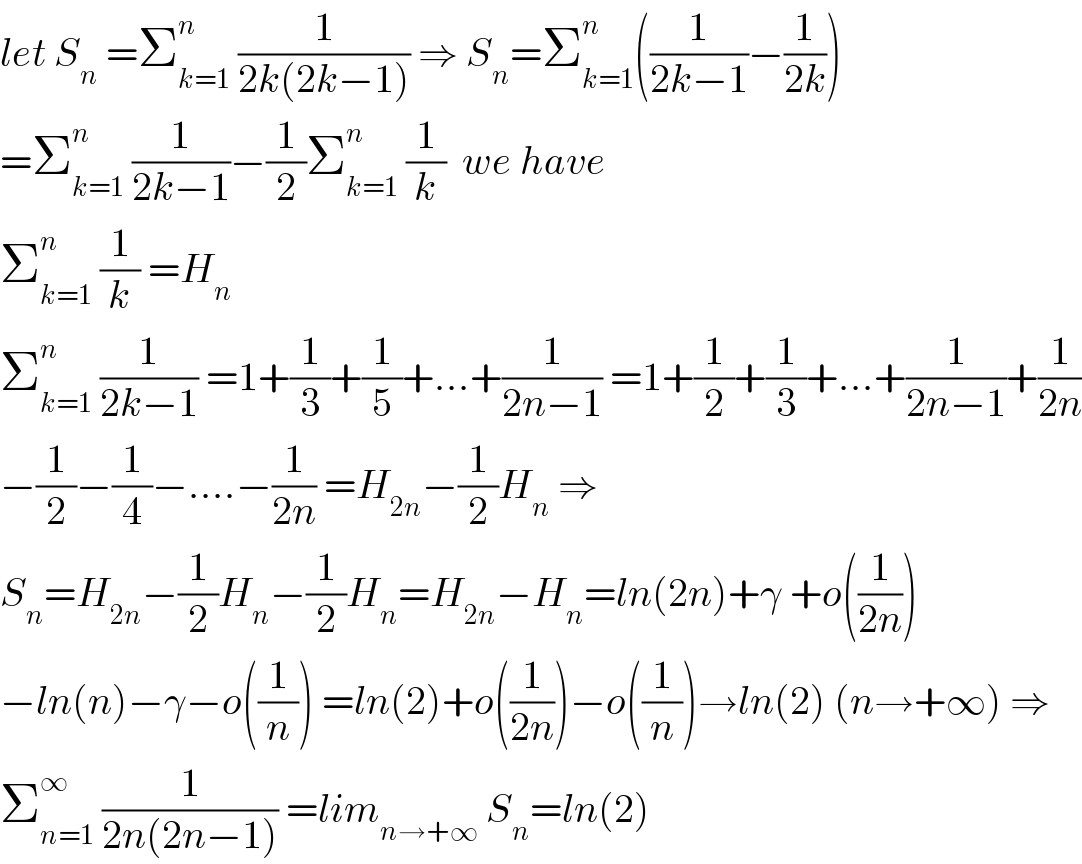
$${let}\:{S}_{{n}} \:=\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{1}}{\mathrm{2}{k}\left(\mathrm{2}{k}−\mathrm{1}\right)}\:\Rightarrow\:{S}_{{n}} =\sum_{{k}=\mathrm{1}} ^{{n}} \left(\frac{\mathrm{1}}{\mathrm{2}{k}−\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}{k}}\right) \\ $$$$=\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{1}}{\mathrm{2}{k}−\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}}\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{1}}{{k}}\:\:{we}\:{have} \\ $$$$\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{1}}{{k}}\:={H}_{{n}} \\ $$$$\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{1}}{\mathrm{2}{k}−\mathrm{1}}\:=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{5}}+…+\frac{\mathrm{1}}{\mathrm{2}{n}−\mathrm{1}}\:=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}+…+\frac{\mathrm{1}}{\mathrm{2}{n}−\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{2}{n}} \\ $$$$−\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{4}}−….−\frac{\mathrm{1}}{\mathrm{2}{n}}\:={H}_{\mathrm{2}{n}} −\frac{\mathrm{1}}{\mathrm{2}}{H}_{{n}} \:\Rightarrow \\ $$$${S}_{{n}} ={H}_{\mathrm{2}{n}} −\frac{\mathrm{1}}{\mathrm{2}}{H}_{{n}} −\frac{\mathrm{1}}{\mathrm{2}}{H}_{{n}} ={H}_{\mathrm{2}{n}} −{H}_{{n}} ={ln}\left(\mathrm{2}{n}\right)+\gamma\:+{o}\left(\frac{\mathrm{1}}{\mathrm{2}{n}}\right) \\ $$$$−{ln}\left({n}\right)−\gamma−{o}\left(\frac{\mathrm{1}}{{n}}\right)\:={ln}\left(\mathrm{2}\right)+{o}\left(\frac{\mathrm{1}}{\mathrm{2}{n}}\right)−{o}\left(\frac{\mathrm{1}}{{n}}\right)\rightarrow{ln}\left(\mathrm{2}\right)\:\left({n}\rightarrow+\infty\right)\:\Rightarrow \\ $$$$\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{2}{n}\left(\mathrm{2}{n}−\mathrm{1}\right)}\:={lim}_{{n}\rightarrow+\infty} \:{S}_{{n}} ={ln}\left(\mathrm{2}\right) \\ $$
Commented by Tony Lin last updated on 25/Apr/20

$${thanks}\:{sir} \\ $$
