prove-that-n-2-gt-n-5-for-integral-n-3-

Question Number 25170 by NECx last updated on 05/Dec/17

p r o v e t h a t n^{2} > n - 5 f o r i n t e g r a l

n ⩾ 3

Commented by mrW1 last updated on 06/Dec/17

m a y b e t h e q u e s t i o n i s

n^{2} > n + 5 f o r n ⩾ 3

Commented by jota@ last updated on 11/Dec/17

Y e s

Answered by jota+ last updated on 09/Dec/17

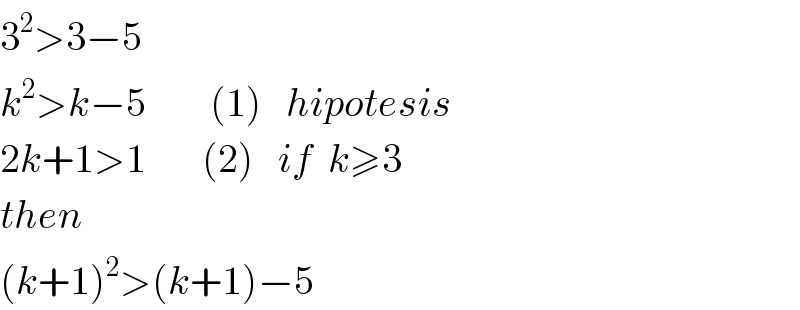
3^{2} > 3 - 5

k^{2} > k - 5 (1) h i p o t e s i s

2 k + 1 > 1 (2) i f k ⩾ 3

t h e n

{(k + 1)}^{2} > (k + 1) - 5

Commented by NECx last updated on 06/Dec/17

t h a n k y o u s o m u c h

Answered by mrW1 last updated on 05/Dec/17

n^{2} = n \times n ⩾ 3 n = n + 2 n ⩾ n + 6 > n - 5

Facebook Tweet Pin