Question Number 164821 by mathls last updated on 22/Jan/22
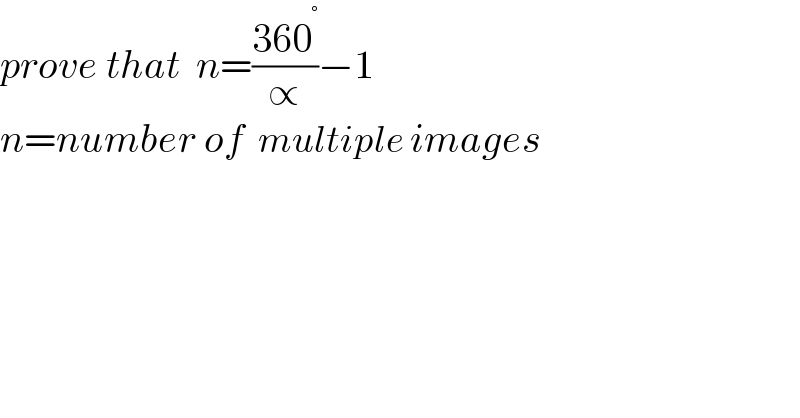
$${prove}\:{that}\:\:{n}=\frac{\mathrm{360}^{°} }{\propto}−\mathrm{1} \\ $$$${n}={number}\:{of}\:\:{multiple}\:{images}\: \\ $$
Commented by mathls last updated on 22/Jan/22

$${please}\:{i}\:{have}\:{problem}\:{and}\:{need}\:{to}\:{your} \\ $$$${help}. \\ $$
Commented by MJS_new last updated on 22/Jan/22
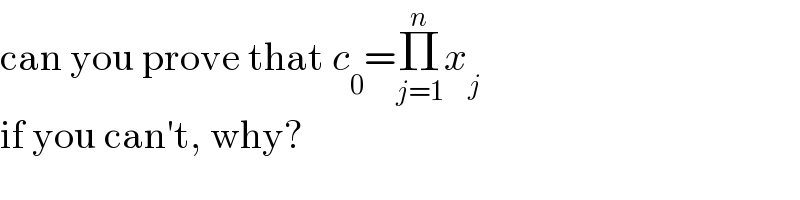
$$\mathrm{can}\:\mathrm{you}\:\mathrm{prove}\:\mathrm{that}\:{c}_{\mathrm{0}} =\underset{{j}=\mathrm{1}} {\overset{{n}} {\prod}}{x}_{{j}} \\ $$$$\mathrm{if}\:\mathrm{you}\:\mathrm{can}'\mathrm{t},\:\mathrm{why}? \\ $$
Commented by mr W last updated on 23/Jan/22

$${the}\:{forum}\:{is}\:{not}\:{good}\:{place}\:{for}\:{such} \\ $$$${general}\:{or}\:{basic}\:\:{questions},\:{just}\:{like} \\ $$$${how}\:{to}\:{prove}\:{E}={mc}^{\mathrm{2}} .\:{Google}\:{is}\:{the} \\ $$$${right}\:{place}\:{to}\:{go},\:{as}\:{i}\:{have}\:{suggested}. \\ $$$${but}\:{i}\:{guess}\:{you}\:{wont}\:{follow}\:{my} \\ $$$${suggestion}. \\ $$
Commented by mathls last updated on 23/Jan/22
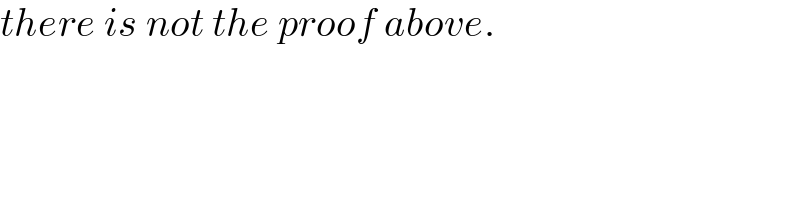
$${there}\:{is}\:{not}\:{the}\:{proof}\:{above}. \\ $$
Commented by mr W last updated on 24/Jan/22

$${i}\:{think}\:{it}\:{depends}\:{on}\:{what}\:{you}\:{think} \\ $$$${is}\:{a}\:{proof}.\:{i}\:{think}\:{you}\:{can}\:{also}\:{not} \\ $$$${find}\:{in}\:{google}\:{a}\:“{proof}''\:{for}\: \\ $$$${a}\left({b}+{c}\right)={ab}+{ac}. \\ $$$$ \\ $$$${it}\:{is}\:{easy}\:{to}\:{understand}\:{the}\:{number} \\ $$$${of}\:{multiple}\:{images}\:{in}\:{two}\:{adjacent} \\ $$$${mirrors}\:{with}\:{an}\:{angle}\:\theta\:{between}\:{them}. \\ $$$${if}\:\theta\:{divides}\:\mathrm{360}°,\:{then}\:{we}\:{can}\:{see}\:{that} \\ $$$${the}\:{whole}\:{circle}\:\left(\mathrm{360}°\right)\:{can}\:{be}\:{divided} \\ $$$${into}\:\frac{\mathrm{360}°}{\theta}\:{equal}\:{parts}.\:{each}\:{part}\:{is}\:{the} \\ $$$${image}\:{of}\:{the}\:{others}.\:{we}\:{have}\:{thus} \\ $$$${totally}\:\frac{\mathrm{360}°}{\theta}\:{objects}.\:{since}\:{one}\:{object} \\ $$$${is}\:{the}\:{real}\:{object},\:{the}\:{others}\:{are}\:{just} \\ $$$${the}\:{reflection}\:{of}\:{the}\:{reflection}\:{of} \\ $$$${the}\:{reflection}\:{etc}.\:{of}\:{the}\:{real}\:{object}. \\ $$$${that}\:{means}\:{the}\:{number}\:{of}\:{images} \\ $$$${is}\:\frac{\mathrm{360}°}{\theta}−\mathrm{1}.\:{i}\:{know}\:{you}\:{wont}\:{think}\: \\ $$$${this}\:{is}\:{a}\:{proof}. \\ $$
Commented by mr W last updated on 24/Jan/22

Commented by mathls last updated on 24/Jan/22
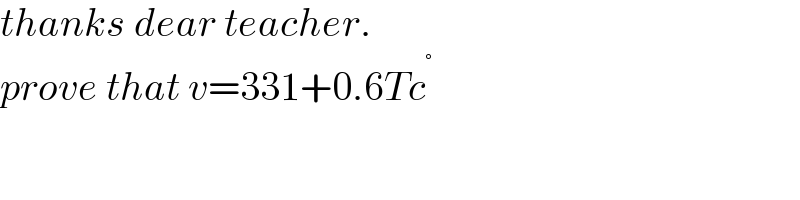
$${thanks}\:{dear}\:{teacher}. \\ $$$${prove}\:{that}\:{v}=\mathrm{331}+\mathrm{0}.\mathrm{6}{Tc}^{°} \: \\ $$
Commented by mr W last updated on 24/Jan/22
$${please}\:{don}'{t}\:{put}\:{such}\:{questions} \\ $$$${without}\:{saying}\:{what}\:{they}\:{are}\:{about}! \\ $$
Commented by mathls last updated on 24/Jan/22
$${speed}\:{of}\:{sound}\:{in}\:{air}. \\ $$
