Question Number 30217 by abdo imad last updated on 18/Feb/18
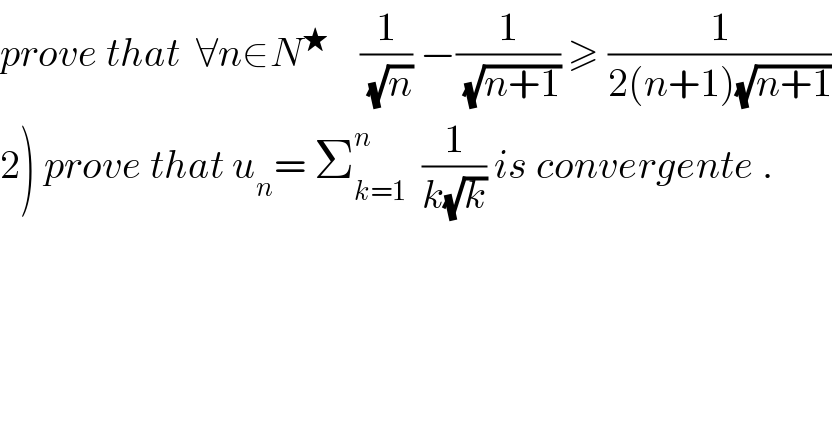
$${prove}\:{that}\:\:\forall{n}\in{N}^{\bigstar} \:\:\:\:\frac{\mathrm{1}}{\:\sqrt{{n}}}\:−\frac{\mathrm{1}}{\:\sqrt{{n}+\mathrm{1}}}\:\geqslant\:\frac{\mathrm{1}}{\mathrm{2}\left({n}+\mathrm{1}\right)\sqrt{{n}+\mathrm{1}}} \\ $$$$\left.\mathrm{2}\right)\:{prove}\:{that}\:{u}_{{n}} =\:\sum_{{k}=\mathrm{1}} ^{{n}} \:\:\frac{\mathrm{1}}{{k}\sqrt{{k}}}\:{is}\:{convergente}\:. \\ $$
