Question Number 165328 by mnjuly1970 last updated on 30/Jan/22
$$ \\ $$$$\:\:\:\:\:{prove}\:{that} \\ $$$$\:\: \\ $$$$\:\:\:\:\:\:\:\mathscr{N}{ice}\:\:\:\mathscr{I}{ntegral} \\ $$$$\:\:\:\:\:\:\:\boldsymbol{\phi}=\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\:{tan}^{\:β\mathrm{1}} \:\left({x}^{\:\frac{\mathrm{3}}{\mathrm{2}}} \right)}{{x}^{\:\mathrm{2}} }\:{dx}\:\:=\frac{\pi\:+\:\sqrt{\mathrm{3}}\:{ln}\left(\mathrm{7}\:+\mathrm{4}\sqrt{\mathrm{3}}\:\right)}{\mathrm{4}}\:\:\:\:\:\:\:\:\:\:\:\:\:\blacksquare\:\:{m}.{n} \\ $$$$\:\:\:\:\:\:βββββββββ\:\:\: \\ $$
Answered by Lordose last updated on 30/Jan/22
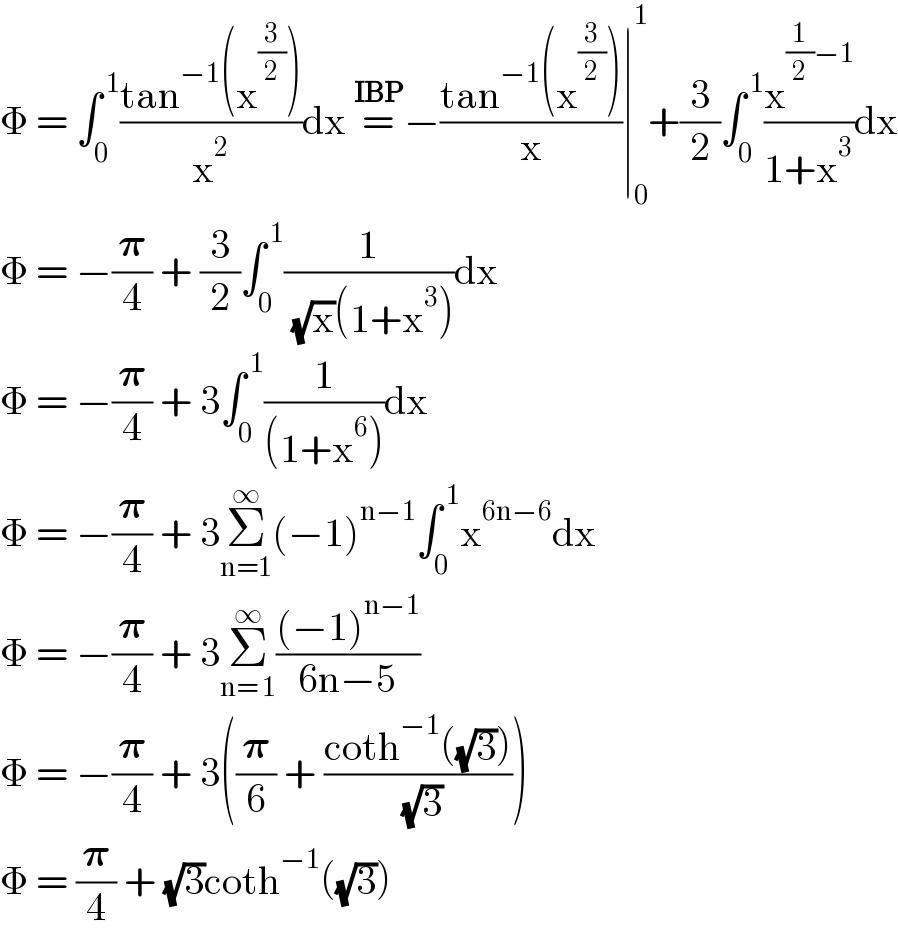
$$\Phi\:=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{tan}^{β\mathrm{1}} \left(\mathrm{x}^{\frac{\mathrm{3}}{\mathrm{2}}} \right)}{\mathrm{x}^{\mathrm{2}} }\mathrm{dx}\:\overset{\boldsymbol{\mathrm{IBP}}} {=}β\frac{\mathrm{tan}^{β\mathrm{1}} \left(\mathrm{x}^{\frac{\mathrm{3}}{\mathrm{2}}} \right)}{\mathrm{x}}\mid_{\mathrm{0}} ^{\mathrm{1}} +\frac{\mathrm{3}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{x}^{\frac{\mathrm{1}}{\mathrm{2}}β\mathrm{1}} }{\mathrm{1}+\mathrm{x}^{\mathrm{3}} }\mathrm{dx} \\ $$$$\Phi\:=\:β\frac{\boldsymbol{\pi}}{\mathrm{4}}\:+\:\frac{\mathrm{3}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{1}}{\:\sqrt{\mathrm{x}}\left(\mathrm{1}+\mathrm{x}^{\mathrm{3}} \right)}\mathrm{dx} \\ $$$$\Phi\:=\:β\frac{\boldsymbol{\pi}}{\mathrm{4}}\:+\:\mathrm{3}\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{1}}{\left(\mathrm{1}+\mathrm{x}^{\mathrm{6}} \right)}\mathrm{dx} \\ $$$$\Phi\:=\:β\frac{\boldsymbol{\pi}}{\mathrm{4}}\:+\:\mathrm{3}\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(β\mathrm{1}\right)^{\mathrm{n}β\mathrm{1}} \int_{\mathrm{0}} ^{\:\mathrm{1}} \mathrm{x}^{\mathrm{6n}β\mathrm{6}} \mathrm{dx} \\ $$$$\Phi\:=\:β\frac{\boldsymbol{\pi}}{\mathrm{4}}\:+\:\mathrm{3}\underset{\mathrm{n}=\:\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(β\mathrm{1}\right)^{\mathrm{n}β\mathrm{1}} }{\mathrm{6n}β\mathrm{5}} \\ $$$$\Phi\:=\:β\frac{\boldsymbol{\pi}}{\mathrm{4}}\:+\:\mathrm{3}\left(\frac{\boldsymbol{\pi}}{\mathrm{6}}\:+\:\frac{\mathrm{coth}^{β\mathrm{1}} \left(\sqrt{\mathrm{3}}\right)}{\:\sqrt{\mathrm{3}}}\right) \\ $$$$\Phi\:=\:\frac{\boldsymbol{\pi}}{\mathrm{4}}\:+\:\sqrt{\mathrm{3}}\mathrm{coth}^{β\mathrm{1}} \left(\sqrt{\mathrm{3}}\right) \\ $$
Answered by mnjuly1970 last updated on 30/Jan/22
![βββ solutionβββ π=^(i.b.p) [((β1)/x) tan^( β1) ( x^( (3/2)) )]_0 ^1 + (3/2) β«_0 ^( 1) (1/( (βx) .( 1 + x^( 3) ))) dx = β(Ο/4) + (3/2) Ξ© where Ξ© = β«_0 ^( 1) (( dx)/( (βx) (1 +x^( 3) ))) Ξ© =^((βx) =t) β«_0 ^( 1) (( 2)/(1 + x^( 6) )) dx =β«_0 ^( 1) (( x^( 4) +1 β (x^( 4) β1 ))/(1+ x^( 6) )) dx = β«_0 ^( 1) (( (x^( 4) βx^( 2) +1) + x^( 2) )/(1 + x^( 6) ))dx + β«_0 ^( 1) ((1βx^( 2) )/(1 βx^( 2) + x^( 4) )) dx = (Ο/4) + β«_0 ^( 1) (( 3x^( 2) )/( 1+ (x^( 3) )^( 2) )) dx ββ«_0 ^( 1) ((1β x^( β2) )/(( x + x^( β1) )^( 2) β3))dx = (Ο/4) + (Ο/( 4 )) + β«_2 ^( β) (( dx)/(x^( 2) β3)) = (Ο/2) + β«_2 ^( β) (dx/(( x β(β3) )( x +(β3) ))) = (Ο/2) + (1/(2(β3))) { [ln(((xβ(β3))/(x+(β3))) )]_2 ^β } = (Ο/2) + (1/(2(β3))) ln(((2+(β3))/(2β(β3))) ) = (Ο/2) + (1/(2(β3))) ln (7 +4 (β3) ) β΄ π = (Ο/4) + ((β3)/4) ln ( 7 + 4 (β3) ) β m.n](https://www.tinkutara.com/question/Q165341.png)
$$\:\:\:\:\:\:\:\:\:\:βββ\:{solution}βββ \\ $$$$\:\:\:\:\:\:\boldsymbol{\phi}\overset{{i}.{b}.{p}} {=}\:\left[\frac{β\mathrm{1}}{{x}}\:{tan}^{\:β\mathrm{1}} \:\left(\:{x}^{\:\frac{\mathrm{3}}{\mathrm{2}}} \right)\right]_{\mathrm{0}} ^{\mathrm{1}} +\:\frac{\mathrm{3}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \:\frac{\mathrm{1}}{\:\sqrt{{x}}\:.\left(\:\mathrm{1}\:+\:{x}^{\:\mathrm{3}} \right)}\:{dx} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\:β\frac{\pi}{\mathrm{4}}\:\:+\:\frac{\mathrm{3}}{\mathrm{2}}\:\Omega\:\:\:\:{where}\:\:\Omega\:=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\:{dx}}{\:\sqrt{{x}}\:\left(\mathrm{1}\:+{x}^{\:\mathrm{3}} \right)} \\ $$$$\:\:\:\:\Omega\:\overset{\sqrt{{x}}\:={t}} {=}\:\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\:\mathrm{2}}{\mathrm{1}\:+\:{x}^{\:\mathrm{6}} }\:{dx}\:=\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\:{x}^{\:\mathrm{4}} +\mathrm{1}\:β\:\left({x}^{\:\mathrm{4}} β\mathrm{1}\:\right)}{\mathrm{1}+\:{x}^{\:\mathrm{6}} }\:{dx} \\ $$$$\:\:\:\:\:\:\:\:\:=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\:\left({x}^{\:\mathrm{4}} β{x}^{\:\mathrm{2}} +\mathrm{1}\right)\:+\:{x}^{\:\mathrm{2}} }{\mathrm{1}\:+\:{x}^{\:\mathrm{6}} }{dx}\:+\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{1}β{x}^{\:\mathrm{2}} }{\mathrm{1}\:β{x}^{\:\mathrm{2}} +\:{x}^{\:\mathrm{4}} }\:{dx} \\ $$$$\:\:\:\:\:\:=\:\:\:\frac{\pi}{\mathrm{4}}\:+\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\:\mathrm{3}{x}^{\:\mathrm{2}} }{\:\mathrm{1}+\:\left({x}^{\:\mathrm{3}} \right)^{\:\mathrm{2}} }\:{dx}\:β\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{1}β\:{x}^{\:β\mathrm{2}} }{\left(\:{x}\:+\:{x}^{\:β\mathrm{1}} \right)^{\:\mathrm{2}} β\mathrm{3}}{dx} \\ $$$$\:\:\:\:\:=\:\frac{\pi}{\mathrm{4}}\:\:+\:\frac{\pi}{\:\:\:\mathrm{4}\:\:}\:+\:\int_{\mathrm{2}} ^{\:\infty} \frac{\:{dx}}{{x}^{\:\mathrm{2}} β\mathrm{3}} \\ $$$$\:\:\:\:\:\:=\:\frac{\pi}{\mathrm{2}}\:\:+\:\int_{\mathrm{2}} ^{\:\infty} \:\frac{{dx}}{\left(\:{x}\:β\sqrt{\mathrm{3}}\:\right)\left(\:{x}\:+\sqrt{\mathrm{3}}\:\right)} \\ $$$$\:\:\:\:\:\:=\:\frac{\pi}{\mathrm{2}}\:\:+\:\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}\:\left\{\:\left[{ln}\left(\frac{{x}β\sqrt{\mathrm{3}}}{{x}+\sqrt{\mathrm{3}}}\:\right)\right]_{\mathrm{2}} ^{\infty} \right\} \\ $$$$\:\:\:\:\:\:\:\:=\:\frac{\pi}{\mathrm{2}}\:+\:\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}\:{ln}\left(\frac{\mathrm{2}+\sqrt{\mathrm{3}}}{\mathrm{2}β\sqrt{\mathrm{3}}}\:\right) \\ $$$$\:\:\:\:\:\:\:\:\:=\:\frac{\pi}{\mathrm{2}}\:+\:\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}\:{ln}\:\left(\mathrm{7}\:+\mathrm{4}\:\sqrt{\mathrm{3}}\:\right) \\ $$$$\:\:\:\:\:\:\:\therefore\:\:\:\:\boldsymbol{\phi}\:=\:\frac{\pi}{\mathrm{4}}\:+\:\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}\:{ln}\:\left(\:\mathrm{7}\:+\:\mathrm{4}\:\sqrt{\mathrm{3}}\:\right)\:\:\:\blacksquare\:{m}.{n}\:\:\:\:\:\: \\ $$$$\:\: \\ $$
Answered by Ar Brandon last updated on 30/Jan/22
![π=β«_0 ^1 ((tan^(β1) (x^(3/2) ))/x^2 )dx=β[(1/x)tan^(β1) (x^(3/2) )]_0 ^1 +(3/2)β«_0 ^1 (x^(β(1/2)) /(1+x^3 ))dx =β(Ο/4)+3β«_0 ^1 (dt/(1+t^6 ))=β(Ο/4)+3β«_0 ^1 (dt/((t^2 +1)(t^4 βt^2 +1))) =β(Ο/4)+β«_0 ^1 ((1/(t^2 +1))β((t^2 β2)/(t^4 βt^2 +1)))dt=β(Ο/4)+(Ο/4)ββ«_0 ^1 ((t^2 β2)/(t^4 βt^2 +1))dt =β(1/2)β«_0 ^1 ((3(t^2 β1)β(t^2 +1))/(t^4 βt^2 +1))dt=(1/2)β«_0 ^1 ((t^2 +1)/(t^4 βt^2 +1))dtβ(3/2)β«_0 ^1 ((t^2 β1)/(t^4 βt^2 +1))dt =(1/2)β«_0 ^1 ((1+(1/t^2 ))/((tβ(1/t))^2 +1))dtβ(3/2)β«_0 ^1 ((1β(1/t^2 ))/((t+(1/t))^2 β3))dt =(1/2)[arctan(((t^2 β1)/t))]_0 ^1 +((β3)/4)[lnβ£((t^2 +(β3)t+1)/(t^2 β(β3)t+1))β£]_0 ^1 =(1/2)((Ο/2))+((β3)/4)lnβ£((2+(β3))/(2β(β3)))β£=(Ο/4)+((β3)/4)ln(2+(β3))^2 =(Ο/4)+((β3)/4)ln(7+4(β3))](https://www.tinkutara.com/question/Q165346.png)
$$\boldsymbol{\phi}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{tan}^{β\mathrm{1}} \left({x}^{\frac{\mathrm{3}}{\mathrm{2}}} \right)}{{x}^{\mathrm{2}} }{dx}=β\left[\frac{\mathrm{1}}{{x}}\mathrm{tan}^{β\mathrm{1}} \left({x}^{\frac{\mathrm{3}}{\mathrm{2}}} \right)\right]_{\mathrm{0}} ^{\mathrm{1}} +\frac{\mathrm{3}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{β\frac{\mathrm{1}}{\mathrm{2}}} }{\mathrm{1}+{x}^{\mathrm{3}} }{dx} \\ $$$$\:\:\:\:=β\frac{\pi}{\mathrm{4}}+\mathrm{3}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dt}}{\mathrm{1}+{t}^{\mathrm{6}} }=β\frac{\pi}{\mathrm{4}}+\mathrm{3}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dt}}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)\left({t}^{\mathrm{4}} β{t}^{\mathrm{2}} +\mathrm{1}\right)} \\ $$$$\:\:\:\:=β\frac{\pi}{\mathrm{4}}+\int_{\mathrm{0}} ^{\mathrm{1}} \left(\frac{\mathrm{1}}{{t}^{\mathrm{2}} +\mathrm{1}}β\frac{{t}^{\mathrm{2}} β\mathrm{2}}{{t}^{\mathrm{4}} β{t}^{\mathrm{2}} +\mathrm{1}}\right){dt}=β\frac{\pi}{\mathrm{4}}+\frac{\pi}{\mathrm{4}}β\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{t}^{\mathrm{2}} β\mathrm{2}}{{t}^{\mathrm{4}} β{t}^{\mathrm{2}} +\mathrm{1}}{dt} \\ $$$$\:\:\:\:=β\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{3}\left({t}^{\mathrm{2}} β\mathrm{1}\right)β\left({t}^{\mathrm{2}} +\mathrm{1}\right)}{{t}^{\mathrm{4}} β{t}^{\mathrm{2}} +\mathrm{1}}{dt}=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{t}^{\mathrm{2}} +\mathrm{1}}{{t}^{\mathrm{4}} β{t}^{\mathrm{2}} +\mathrm{1}}{dt}β\frac{\mathrm{3}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{t}^{\mathrm{2}} β\mathrm{1}}{{t}^{\mathrm{4}} β{t}^{\mathrm{2}} +\mathrm{1}}{dt} \\ $$$$\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}+\frac{\mathrm{1}}{{t}^{\mathrm{2}} }}{\left({t}β\frac{\mathrm{1}}{{t}}\right)^{\mathrm{2}} +\mathrm{1}}{dt}β\frac{\mathrm{3}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}β\frac{\mathrm{1}}{{t}^{\mathrm{2}} }}{\left({t}+\frac{\mathrm{1}}{{t}}\right)^{\mathrm{2}} β\mathrm{3}}{dt} \\ $$$$\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\left[\mathrm{arctan}\left(\frac{{t}^{\mathrm{2}} β\mathrm{1}}{{t}}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} +\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}\left[\mathrm{ln}\mid\frac{{t}^{\mathrm{2}} +\sqrt{\mathrm{3}}{t}+\mathrm{1}}{{t}^{\mathrm{2}} β\sqrt{\mathrm{3}}{t}+\mathrm{1}}\mid\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\pi}{\mathrm{2}}\right)+\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}\mathrm{ln}\mid\frac{\mathrm{2}+\sqrt{\mathrm{3}}}{\mathrm{2}β\sqrt{\mathrm{3}}}\mid=\frac{\pi}{\mathrm{4}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}\mathrm{ln}\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:=\frac{\pi}{\mathrm{4}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}\mathrm{ln}\left(\mathrm{7}+\mathrm{4}\sqrt{\mathrm{3}}\right) \\ $$
Commented by mnjuly1970 last updated on 31/Jan/22
$${thanks}\:{alot}\:{sir}\:{brandon} \\ $$$$ \\ $$