Question Number 109082 by 1777 last updated on 21/Aug/20
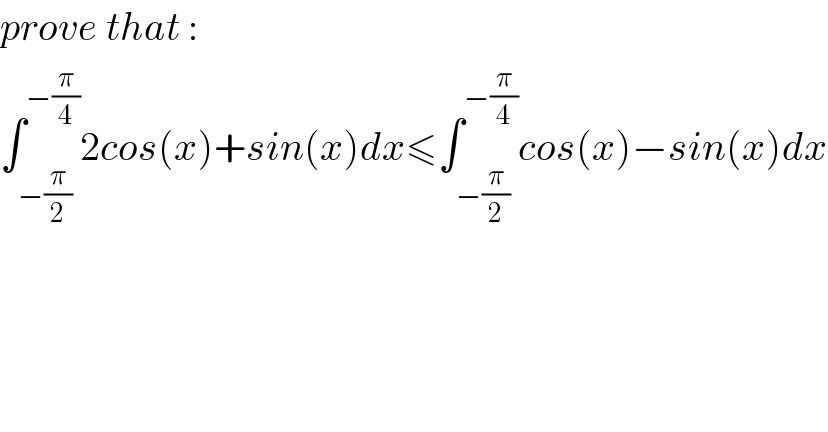
$${prove}\:{that}\:: \\ $$$$\int_{−\frac{\pi}{\mathrm{2}}} ^{−\frac{\pi}{\mathrm{4}}} \mathrm{2}{cos}\left({x}\right)+{sin}\left({x}\right){dx}\leqslant\int_{−\frac{\pi}{\mathrm{2}}} ^{−\frac{\pi}{\mathrm{4}}} {cos}\left({x}\right)−{sin}\left({x}\right){dx} \\ $$
Answered by malwan last updated on 21/Aug/20
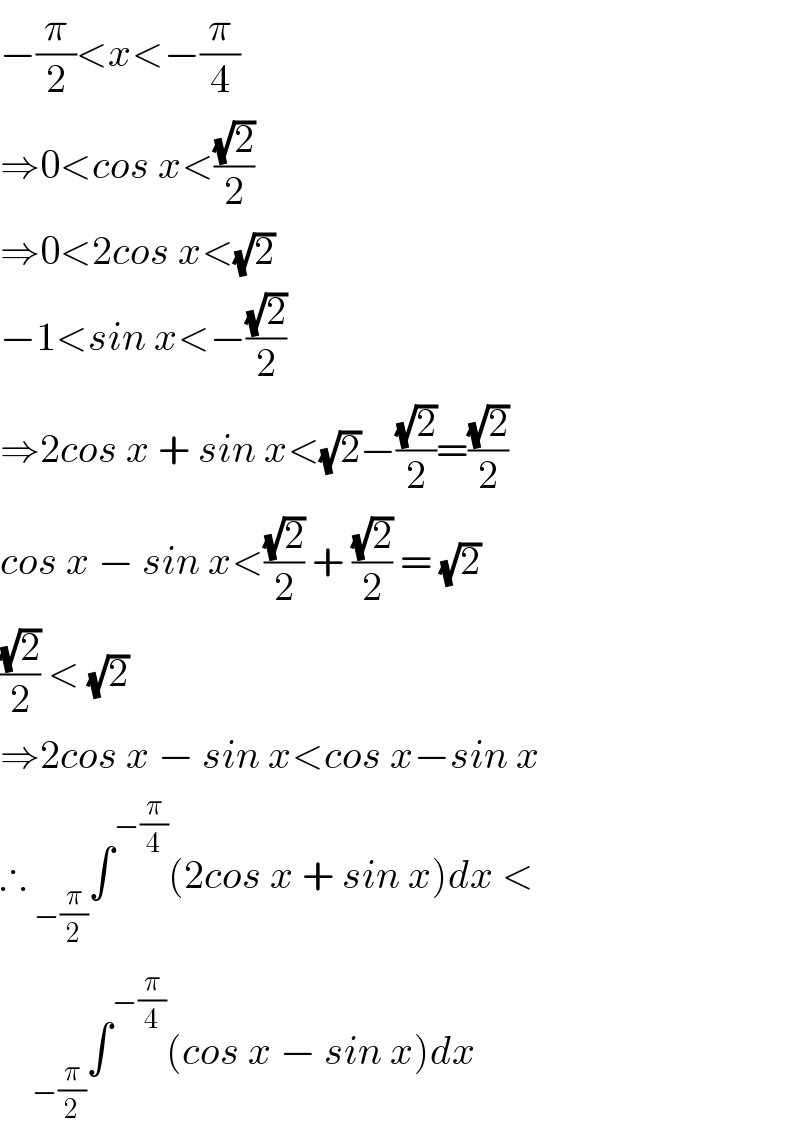
$$−\frac{\pi}{\mathrm{2}}<{x}<−\frac{\pi}{\mathrm{4}} \\ $$$$\Rightarrow\mathrm{0}<{cos}\:{x}<\frac{\sqrt{\mathrm{2}}}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{0}<\mathrm{2}{cos}\:{x}<\sqrt{\mathrm{2}} \\ $$$$−\mathrm{1}<{sin}\:{x}<−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{2}{cos}\:{x}\:+\:{sin}\:{x}<\sqrt{\mathrm{2}}−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}} \\ $$$${cos}\:{x}\:−\:{sin}\:{x}<\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\:+\:\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\:=\:\sqrt{\mathrm{2}} \\ $$$$\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\:<\:\sqrt{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{2}{cos}\:{x}\:−\:{sin}\:{x}<{cos}\:{x}−{sin}\:{x} \\ $$$$\therefore\:_{−\frac{\pi}{\mathrm{2}}} \int^{−\frac{\pi}{\mathrm{4}}} \left(\mathrm{2}{cos}\:{x}\:+\:{sin}\:{x}\right){dx}\:< \\ $$$$\:\:\:\:_{−\frac{\pi}{\mathrm{2}}} \int^{−\frac{\pi}{\mathrm{4}}} \left({cos}\:{x}\:−\:{sin}\:{x}\right){dx} \\ $$
Commented by 1777 last updated on 21/Aug/20
nice
