Question Number 45555 by rahul 19 last updated on 14/Oct/18
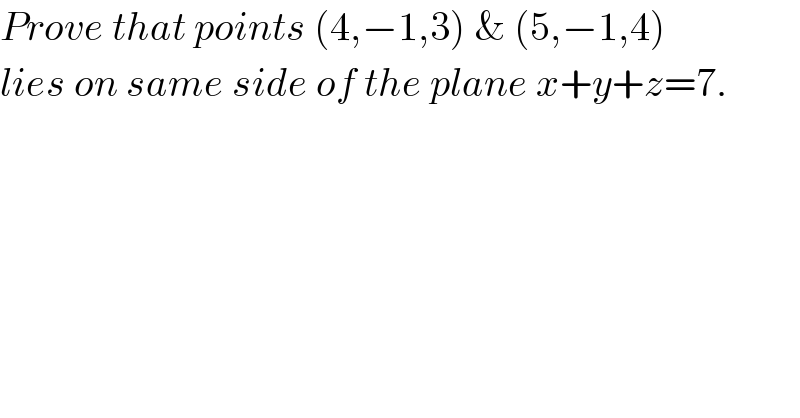
$${Prove}\:{that}\:{points}\:\left(\mathrm{4},−\mathrm{1},\mathrm{3}\right)\:\&\:\left(\mathrm{5},−\mathrm{1},\mathrm{4}\right) \\ $$$${lies}\:{on}\:{same}\:{side}\:{of}\:{the}\:{plane}\:{x}+{y}+{z}=\mathrm{7}. \\ $$
Commented by rahul 19 last updated on 14/Oct/18

Answered by tanmay.chaudhury50@gmail.com last updated on 14/Oct/18
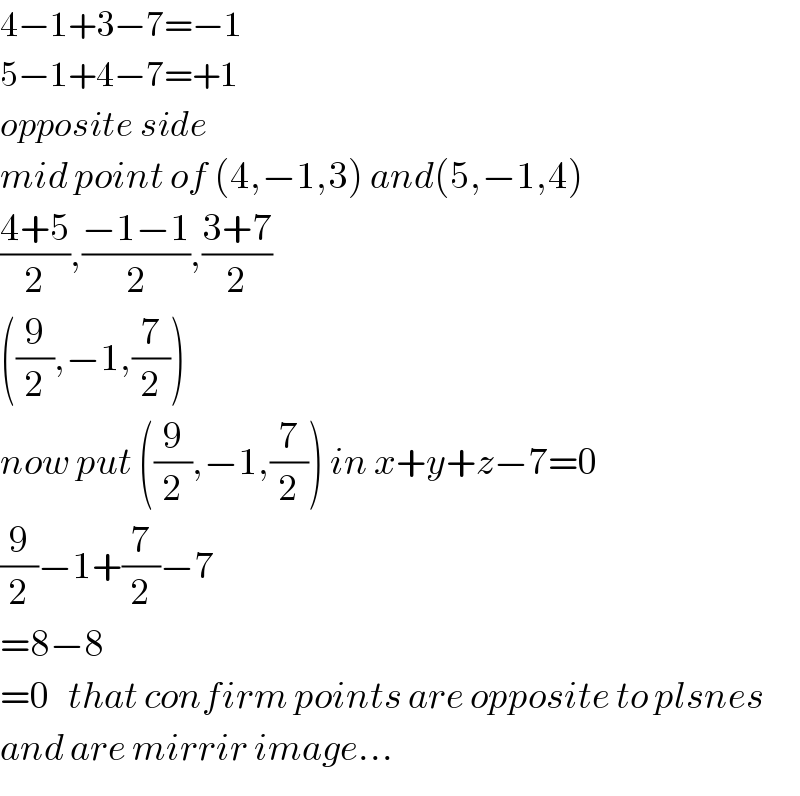
$$\mathrm{4}−\mathrm{1}+\mathrm{3}−\mathrm{7}=−\mathrm{1} \\ $$$$\mathrm{5}−\mathrm{1}+\mathrm{4}−\mathrm{7}=+\mathrm{1} \\ $$$${opposite}\:{side} \\ $$$${mid}\:{point}\:{of}\:\left(\mathrm{4},−\mathrm{1},\mathrm{3}\right)\:{and}\left(\mathrm{5},−\mathrm{1},\mathrm{4}\right) \\ $$$$\frac{\mathrm{4}+\mathrm{5}}{\mathrm{2}},\frac{−\mathrm{1}−\mathrm{1}}{\mathrm{2}},\frac{\mathrm{3}+\mathrm{7}}{\mathrm{2}} \\ $$$$\left(\frac{\mathrm{9}}{\mathrm{2}},−\mathrm{1},\frac{\mathrm{7}}{\mathrm{2}}\right) \\ $$$${now}\:{put}\:\left(\frac{\mathrm{9}}{\mathrm{2}},−\mathrm{1},\frac{\mathrm{7}}{\mathrm{2}}\right)\:{in}\:{x}+{y}+{z}−\mathrm{7}=\mathrm{0} \\ $$$$\frac{\mathrm{9}}{\mathrm{2}}−\mathrm{1}+\frac{\mathrm{7}}{\mathrm{2}}−\mathrm{7} \\ $$$$=\mathrm{8}−\mathrm{8} \\ $$$$=\mathrm{0}\:\:\:{that}\:{confirm}\:{points}\:{are}\:{opposite}\:{to}\:{plsnes} \\ $$$${and}\:{are}\:{mirrir}\:{image}… \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 14/Oct/18
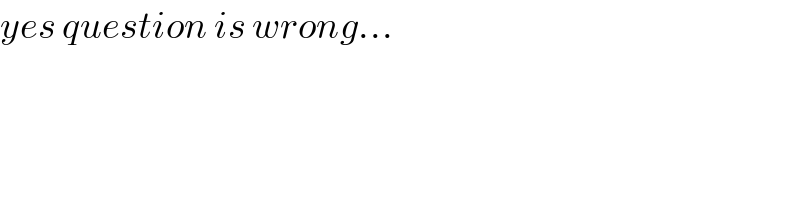
$${yes}\:{question}\:{is}\:{wrong}… \\ $$
