Menu Close

Prove-that-r-1-2n-1-1-r-1-0-1-x-r-1-x-2n-r-dx-0-1-1-x-2n-x-2n-1-x-2n-1-x-2n-1-dx-

Tinku Tara 0 Comments
Pin




Question Number 24142 by Tinkutara last updated on 13/Nov/17
Prove that Σ_(r=1) ^(2n−1) (−1)^(r−1) (∫_0 ^1 x^r (1−x)^(2n−r) dx) =∫_0 ^1 [(1−x)^(2n) +x^(2n) −(1−x)^(2n+1) −x^(2n+1) ]dx
$${Prove}\:{that} \\ $$$$\underset{{r}=\mathrm{1}} {\overset{\mathrm{2}{n}−\mathrm{1}} {\sum}}\left(−\mathrm{1}\right)^{{r}−\mathrm{1}} \left(\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}{x}^{{r}} \left(\mathrm{1}−{x}\right)^{\mathrm{2}{n}−{r}} {dx}\right) \\ $$$$=\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\left[\left(\mathrm{1}−{x}\right)^{\mathrm{2}{n}} +{x}^{\mathrm{2}{n}} −\left(\mathrm{1}−{x}\right)^{\mathrm{2}{n}+\mathrm{1}} −{x}^{\mathrm{2}{n}+\mathrm{1}} \right]{dx} \\ $$
Commented by Tinkutara last updated on 13/Nov/17
Thank you very much Sir!
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}! \\ $$
Commented by moxhix last updated on 13/Nov/17
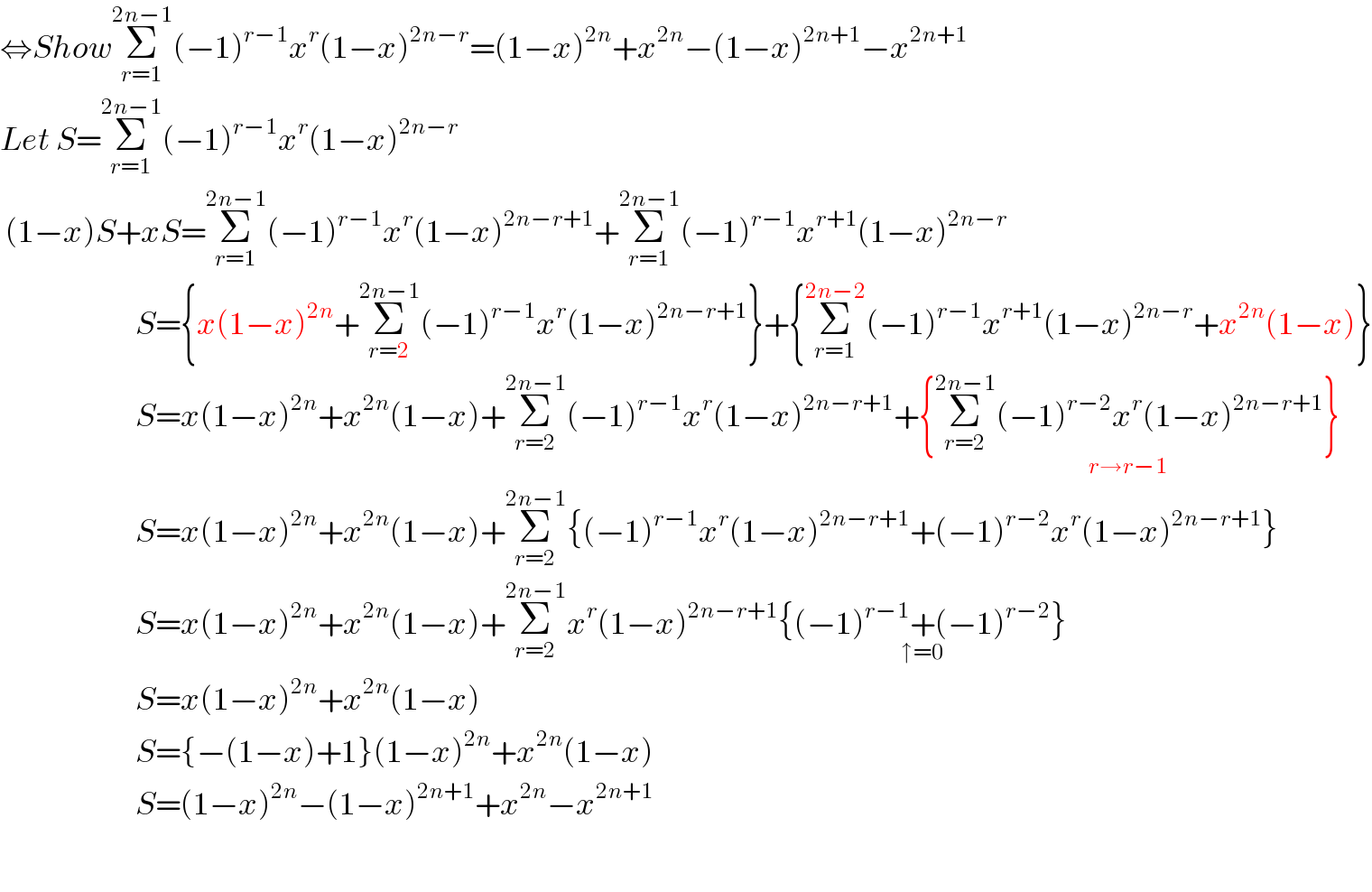
⇔ShowΣ_(r=1) ^(2n−1) (−1)^(r−1) x^r (1−x)^(2n−r) =(1−x)^(2n) +x^(2n) −(1−x)^(2n+1) −x^(2n+1) Let S=Σ_(r=1) ^(2n−1) (−1)^(r−1) x^r (1−x)^(2n−r) (1−x)S+xS=Σ_(r=1) ^(2n−1) (−1)^(r−1) x^r (1−x)^(2n−r+1) +Σ_(r=1) ^(2n−1) (−1)^(r−1) x^(r+1) (1−x)^(2n−r) S={x(1−x)^(2n) +Σ_(r=2) ^(2n−1) (−1)^(r−1) x^r (1−x)^(2n−r+1) }+{Σ_(r=1) ^(2n−2) (−1)^(r−1) x^(r+1) (1−x)^(2n−r) +x^(2n) (1−x)} S=x(1−x)^(2n) +x^(2n) (1−x)+Σ_(r=2) ^(2n−1) (−1)^(r−1) x^r (1−x)^(2n−r+1) +{Σ_(r=2) ^(2n−1) (−1)^(r−2) x^r (1−x)^(2n−r+1) }_(r→r−1) S=x(1−x)^(2n) +x^(2n) (1−x)+Σ_(r=2) ^(2n−1) {(−1)^(r−1) x^r (1−x)^(2n−r+1) +(−1)^(r−2) x^r (1−x)^(2n−r+1) } S=x(1−x)^(2n) +x^(2n) (1−x)+Σ_(r=2) ^(2n−1) x^r (1−x)^(2n−r+1) {(−1)^(r−1) +(−1)^(r−2) }_(↑=0) S=x(1−x)^(2n) +x^(2n) (1−x) S={−(1−x)+1}(1−x)^(2n) +x^(2n) (1−x) S=(1−x)^(2n) −(1−x)^(2n+1) +x^(2n) −x^(2n+1)
$$\Leftrightarrow{Show}\underset{{r}=\mathrm{1}} {\overset{\mathrm{2}{n}−\mathrm{1}} {\sum}}\left(−\mathrm{1}\right)^{{r}−\mathrm{1}} {x}^{{r}} \left(\mathrm{1}−{x}\right)^{\mathrm{2}{n}−{r}} =\left(\mathrm{1}−{x}\right)^{\mathrm{2}{n}} +{x}^{\mathrm{2}{n}} −\left(\mathrm{1}−{x}\right)^{\mathrm{2}{n}+\mathrm{1}} −{x}^{\mathrm{2}{n}+\mathrm{1}} \\ $$$${Let}\:{S}=\underset{{r}=\mathrm{1}} {\overset{\mathrm{2}{n}−\mathrm{1}} {\sum}}\left(−\mathrm{1}\right)^{{r}−\mathrm{1}} {x}^{{r}} \left(\mathrm{1}−{x}\right)^{\mathrm{2}{n}−{r}} \\ $$$$\:\left(\mathrm{1}−{x}\right){S}+{xS}=\underset{{r}=\mathrm{1}} {\overset{\mathrm{2}{n}−\mathrm{1}} {\sum}}\left(−\mathrm{1}\right)^{{r}−\mathrm{1}} {x}^{{r}} \left(\mathrm{1}−{x}\right)^{\mathrm{2}{n}−{r}+\mathrm{1}} +\underset{{r}=\mathrm{1}} {\overset{\mathrm{2}{n}−\mathrm{1}} {\sum}}\left(−\mathrm{1}\right)^{{r}−\mathrm{1}} {x}^{{r}+\mathrm{1}} \left(\mathrm{1}−{x}\right)^{\mathrm{2}{n}−{r}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{S}=\left\{{x}\left(\mathrm{1}−{x}\right)^{\mathrm{2}{n}} +\underset{{r}=\mathrm{2}} {\overset{\mathrm{2}{n}−\mathrm{1}} {\sum}}\left(−\mathrm{1}\right)^{{r}−\mathrm{1}} {x}^{{r}} \left(\mathrm{1}−{x}\right)^{\mathrm{2}{n}−{r}+\mathrm{1}} \right\}+\left\{\underset{{r}=\mathrm{1}} {\overset{\mathrm{2}{n}−\mathrm{2}} {\sum}}\left(−\mathrm{1}\right)^{{r}−\mathrm{1}} {x}^{{r}+\mathrm{1}} \left(\mathrm{1}−{x}\right)^{\mathrm{2}{n}−{r}} +{x}^{\mathrm{2}{n}} \left(\mathrm{1}−{x}\right)\right\} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{S}={x}\left(\mathrm{1}−{x}\right)^{\mathrm{2}{n}} +{x}^{\mathrm{2}{n}} \left(\mathrm{1}−{x}\right)+\underset{{r}=\mathrm{2}} {\overset{\mathrm{2}{n}−\mathrm{1}} {\sum}}\left(−\mathrm{1}\right)^{{r}−\mathrm{1}} {x}^{{r}} \left(\mathrm{1}−{x}\right)^{\mathrm{2}{n}−{r}+\mathrm{1}} +\underset{{r}\rightarrow{r}−\mathrm{1}} {\left\{\underset{{r}=\mathrm{2}} {\overset{\mathrm{2}{n}−\mathrm{1}} {\sum}}\left(−\mathrm{1}\right)^{{r}−\mathrm{2}} {x}^{{r}} \left(\mathrm{1}−{x}\right)^{\mathrm{2}{n}−{r}+\mathrm{1}} \right\}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{S}={x}\left(\mathrm{1}−{x}\right)^{\mathrm{2}{n}} +{x}^{\mathrm{2}{n}} \left(\mathrm{1}−{x}\right)+\underset{{r}=\mathrm{2}} {\overset{\mathrm{2}{n}−\mathrm{1}} {\sum}}\left\{\left(−\mathrm{1}\right)^{{r}−\mathrm{1}} {x}^{{r}} \left(\mathrm{1}−{x}\right)^{\mathrm{2}{n}−{r}+\mathrm{1}} +\left(−\mathrm{1}\right)^{{r}−\mathrm{2}} {x}^{{r}} \left(\mathrm{1}−{x}\right)^{\mathrm{2}{n}−{r}+\mathrm{1}} \right\} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{S}={x}\left(\mathrm{1}−{x}\right)^{\mathrm{2}{n}} +{x}^{\mathrm{2}{n}} \left(\mathrm{1}−{x}\right)+\underset{{r}=\mathrm{2}} {\overset{\mathrm{2}{n}−\mathrm{1}} {\sum}}{x}^{{r}} \left(\mathrm{1}−{x}\right)^{\mathrm{2}{n}−{r}+\mathrm{1}} \underset{\uparrow=\mathrm{0}} {\left\{\left(−\mathrm{1}\right)^{{r}−\mathrm{1}} +\left(−\mathrm{1}\right)^{{r}−\mathrm{2}} \right\}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{S}={x}\left(\mathrm{1}−{x}\right)^{\mathrm{2}{n}} +{x}^{\mathrm{2}{n}} \left(\mathrm{1}−{x}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{S}=\left\{−\left(\mathrm{1}−{x}\right)+\mathrm{1}\right\}\left(\mathrm{1}−{x}\right)^{\mathrm{2}{n}} +{x}^{\mathrm{2}{n}} \left(\mathrm{1}−{x}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{S}=\left(\mathrm{1}−{x}\right)^{\mathrm{2}{n}} −\left(\mathrm{1}−{x}\right)^{\mathrm{2}{n}+\mathrm{1}} +{x}^{\mathrm{2}{n}} −{x}^{\mathrm{2}{n}+\mathrm{1}} \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *