Question Number 116079 by Study last updated on 30/Sep/20
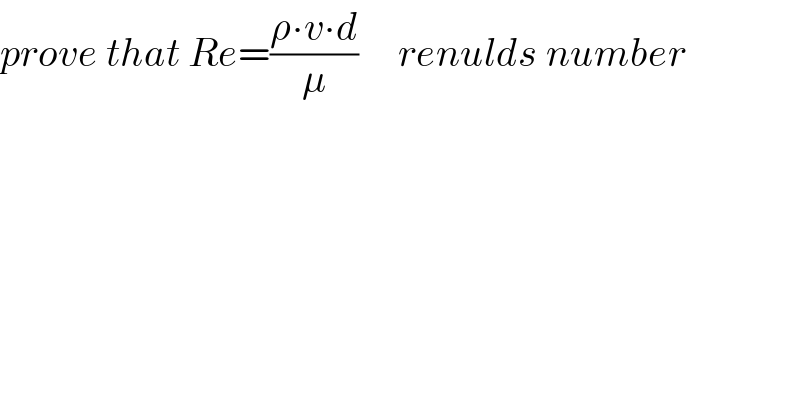
$${prove}\:{that}\:{Re}=\frac{\rho\centerdot{v}\centerdot{d}}{\mu}\:\:\:\:\:{renulds}\:{number} \\ $$
Answered by Olaf last updated on 01/Oct/20

$$\mathrm{It}\:\mathrm{suffices}\:\mathrm{to}\:\mathrm{resize}\:\mathrm{the}\:\mathrm{Navier}−\mathrm{Stokes} \\ $$$$\mathrm{equations}.\:\mathrm{The}\:\mathrm{dimensionless}\:\mathrm{factor} \\ $$$$\frac{\rho{vd}}{\mu}\:\mathrm{appears}\:\mathrm{naturally}.\:\mathrm{This}\:\mathrm{is}\:\mathrm{the} \\ $$$$\mathrm{factor}\:\mathrm{called}\:\mathrm{Reynolds}\:\mathrm{number}. \\ $$
