Question Number 54126 by rahul 19 last updated on 29/Jan/19
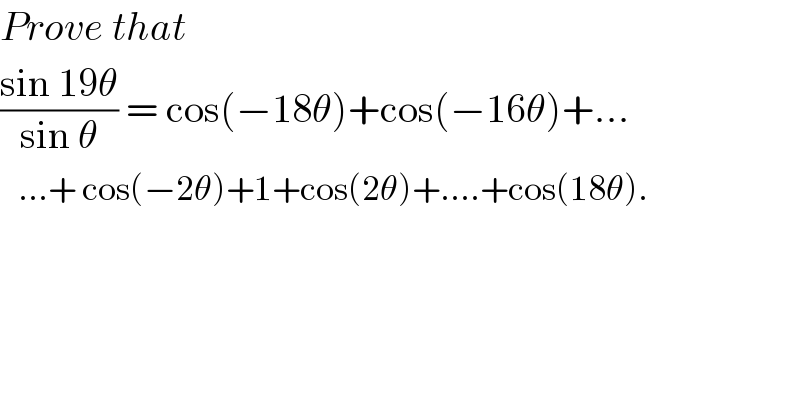
$${Prove}\:{that} \\ $$$$\frac{\mathrm{sin}\:\mathrm{19}\theta}{\mathrm{sin}\:\theta}\:=\:\mathrm{cos}\left(−\mathrm{18}\theta\right)+\mathrm{cos}\left(−\mathrm{16}\theta\right)+… \\ $$$$\:\:\:…+\:\mathrm{cos}\left(−\mathrm{2}\theta\right)+\mathrm{1}+\mathrm{cos}\left(\mathrm{2}\theta\right)+….+\mathrm{cos}\left(\mathrm{18}\theta\right). \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 29/Jan/19
![S=[cos(−18θ)+cos(−16θ)+...+cos(−2θ)]+1+[cos2θ+cos4θ+..+cos18θ] S=S_1 +1+S_2 [S_1 =sum of −ve sngled terms S_2 for +ve angled terms] S_1 =cos(−18θ)+cos(−16θ)+cos(−14θ)+...+cos(−2θ) S_1 =S_2 S=2S_1 +1 now S_1 =cos2θ+cos4θ+cos6θ+...+cos18θ 2sinθcos2θ=sin3θ−sinθ 2sinθcos4θ=sin5θ−sin3θ 2sinθcos6θ=sin7θ−sin5θ ... .... 2sinθcos18θ=sin19θ−sin17θ now addition give →LHS=2sinθ×S_1 during addition the redmarked terms cancelled in right hand side.. so →2sinθ×S_1 =sin19θ−sinθ S_1 =((sin19θ)/(2sinθ))−(1/2) S=2S_1 +1 =2(((sin19θ)/(2sinθ))−(1/2))+1 =((sin19θ)/(sinθ))−1+1 =((sin19θ)/(sinθ)) proved..](https://www.tinkutara.com/question/Q54133.png)
$$ \\ $$$${S}=\left[{cos}\left(−\mathrm{18}\theta\right)+{cos}\left(−\mathrm{16}\theta\right)+…+{cos}\left(−\mathrm{2}\theta\right)\right]+\mathrm{1}+\left[{cos}\mathrm{2}\theta+{cos}\mathrm{4}\theta+..+{cos}\mathrm{18}\theta\right] \\ $$$${S}={S}_{\mathrm{1}} +\mathrm{1}+{S}_{\mathrm{2}} \:\:\left[{S}_{\mathrm{1}} ={sum}\:{of}\:−{ve}\:{sngled}\:{terms}\:\:{S}_{\mathrm{2}} \:\:{for}\:+{ve}\:{angled}\:{terms}\right] \\ $$$${S}_{\mathrm{1}} ={cos}\left(−\mathrm{18}\theta\right)+{cos}\left(−\mathrm{16}\theta\right)+{cos}\left(−\mathrm{14}\theta\right)+…+{cos}\left(−\mathrm{2}\theta\right) \\ $$$${S}_{\mathrm{1}} ={S}_{\mathrm{2}} \\ $$$${S}=\mathrm{2}{S}_{\mathrm{1}} +\mathrm{1} \\ $$$${now} \\ $$$${S}_{\mathrm{1}} ={cos}\mathrm{2}\theta+{cos}\mathrm{4}\theta+{cos}\mathrm{6}\theta+…+{cos}\mathrm{18}\theta \\ $$$$\mathrm{2}{sin}\theta{cos}\mathrm{2}\theta={sin}\mathrm{3}\theta−{sin}\theta \\ $$$$\mathrm{2}{sin}\theta{cos}\mathrm{4}\theta={sin}\mathrm{5}\theta−{sin}\mathrm{3}\theta \\ $$$$\mathrm{2}{sin}\theta{cos}\mathrm{6}\theta={sin}\mathrm{7}\theta−{sin}\mathrm{5}\theta \\ $$$$… \\ $$$$…. \\ $$$$\mathrm{2}{sin}\theta{cos}\mathrm{18}\theta={sin}\mathrm{19}\theta−{sin}\mathrm{17}\theta \\ $$$${now}\:{addition}\:{give}\:\rightarrow{LHS}=\mathrm{2}{sin}\theta×{S}_{\mathrm{1}} \\ $$$${during}\:{addition}\:{the}\:{redmarked}\:{terms}\:{cancelled} \\ $$$${in}\:{right}\:{hand}\:{side}.. \\ $$$${so}\:\rightarrow\mathrm{2}{sin}\theta×{S}_{\mathrm{1}} ={sin}\mathrm{19}\theta−{sin}\theta \\ $$$$\:\:\:\:\:\:\:\:\:\:{S}_{\mathrm{1}} =\frac{{sin}\mathrm{19}\theta}{\mathrm{2}{sin}\theta}−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:{S}=\mathrm{2}{S}_{\mathrm{1}} +\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{2}\left(\frac{{sin}\mathrm{19}\theta}{\mathrm{2}{sin}\theta}−\frac{\mathrm{1}}{\mathrm{2}}\right)+\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{{sin}\mathrm{19}\theta}{{sin}\theta}−\mathrm{1}+\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{{sin}\mathrm{19}\theta}{{sin}\theta}\:\:{proved}.. \\ $$$$ \\ $$$$ \\ $$
Commented by Otchere Abdullai last updated on 29/Jan/19

$${well}\:{done}\:{sir}! \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 29/Jan/19

$${thank}\:{you}\:{sir}… \\ $$
