Question Number 63423 by minh2001 last updated on 04/Jul/19
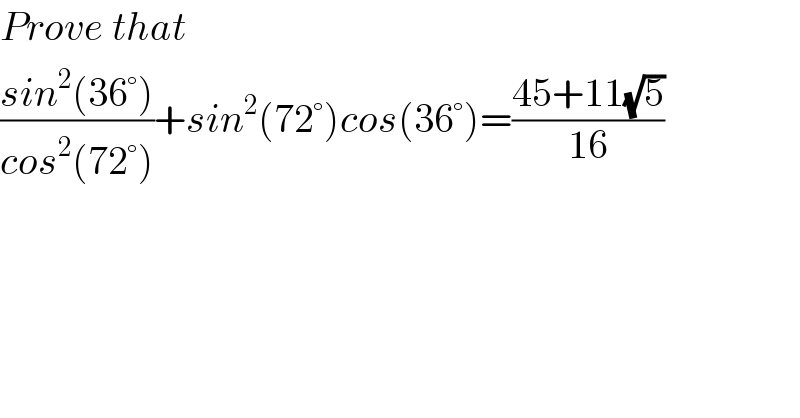
$${Prove}\:{that}\: \\ $$$$\frac{{sin}^{\mathrm{2}} \left(\mathrm{36}°\right)}{{cos}^{\mathrm{2}} \left(\mathrm{72}°\right)}+{sin}^{\mathrm{2}} \left(\mathrm{72}°\right){cos}\left(\mathrm{36}°\right)=\frac{\mathrm{45}+\mathrm{11}\sqrt{\mathrm{5}}}{\mathrm{16}} \\ $$
Commented by Tony Lin last updated on 04/Jul/19
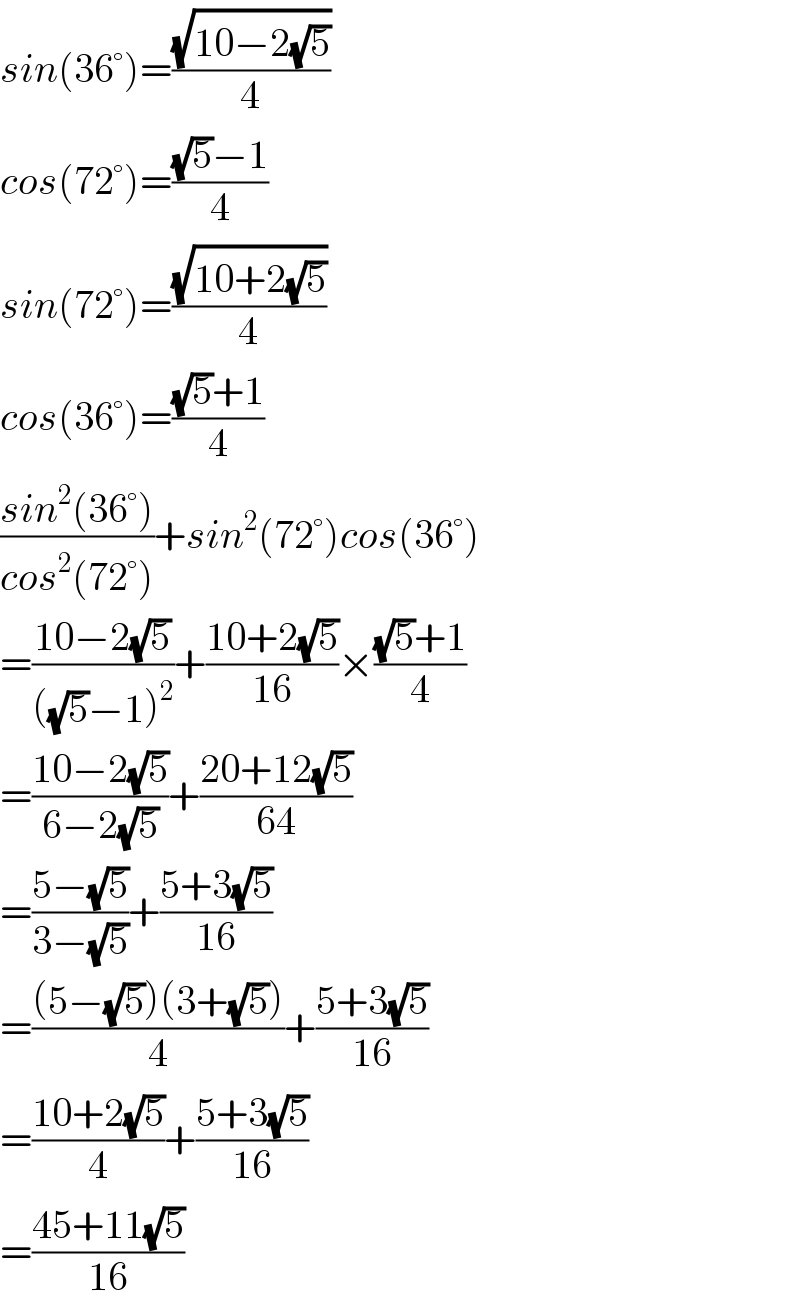
$${sin}\left(\mathrm{36}°\right)=\frac{\sqrt{\mathrm{10}−\mathrm{2}\sqrt{\mathrm{5}}}}{\mathrm{4}} \\ $$$${cos}\left(\mathrm{72}°\right)=\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{4}} \\ $$$${sin}\left(\mathrm{72}°\right)=\frac{\sqrt{\mathrm{10}+\mathrm{2}\sqrt{\mathrm{5}}}}{\mathrm{4}} \\ $$$${cos}\left(\mathrm{36}°\right)=\frac{\sqrt{\mathrm{5}}+\mathrm{1}}{\mathrm{4}} \\ $$$$\frac{{sin}^{\mathrm{2}} \left(\mathrm{36}°\right)}{{cos}^{\mathrm{2}} \left(\mathrm{72}°\right)}+{sin}^{\mathrm{2}} \left(\mathrm{72}°\right){cos}\left(\mathrm{36}°\right) \\ $$$$=\frac{\mathrm{10}−\mathrm{2}\sqrt{\mathrm{5}}}{\left(\sqrt{\mathrm{5}}−\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{10}+\mathrm{2}\sqrt{\mathrm{5}}}{\mathrm{16}}×\frac{\sqrt{\mathrm{5}}+\mathrm{1}}{\mathrm{4}} \\ $$$$=\frac{\mathrm{10}−\mathrm{2}\sqrt{\mathrm{5}}}{\mathrm{6}−\mathrm{2}\sqrt{\mathrm{5}}}+\frac{\mathrm{20}+\mathrm{12}\sqrt{\mathrm{5}}}{\mathrm{64}} \\ $$$$=\frac{\mathrm{5}−\sqrt{\mathrm{5}}}{\mathrm{3}−\sqrt{\mathrm{5}}}+\frac{\mathrm{5}+\mathrm{3}\sqrt{\mathrm{5}}}{\mathrm{16}} \\ $$$$=\frac{\left(\mathrm{5}−\sqrt{\mathrm{5}}\right)\left(\mathrm{3}+\sqrt{\mathrm{5}}\right)}{\mathrm{4}}+\frac{\mathrm{5}+\mathrm{3}\sqrt{\mathrm{5}}}{\mathrm{16}} \\ $$$$=\frac{\mathrm{10}+\mathrm{2}\sqrt{\mathrm{5}}}{\mathrm{4}}+\frac{\mathrm{5}+\mathrm{3}\sqrt{\mathrm{5}}}{\mathrm{16}} \\ $$$$=\frac{\mathrm{45}+\mathrm{11}\sqrt{\mathrm{5}}}{\mathrm{16}} \\ $$
