Question Number 168277 by Eulerian last updated on 07/Apr/22
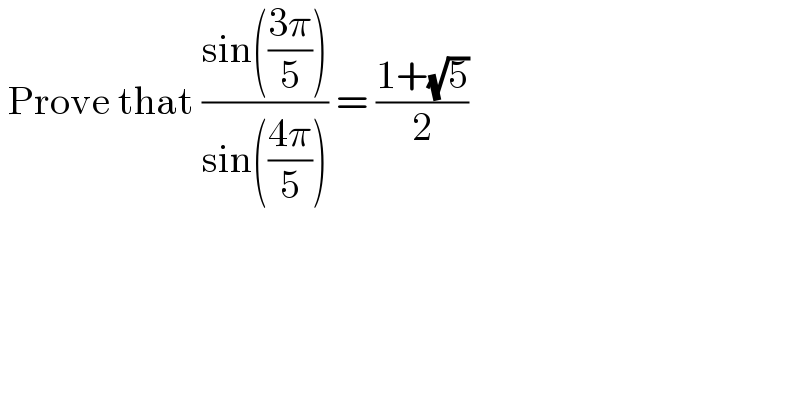
$$\:\mathrm{Prove}\:\mathrm{that}\:\frac{\mathrm{sin}\left(\frac{\mathrm{3}\pi}{\mathrm{5}}\right)}{\mathrm{sin}\left(\frac{\mathrm{4}\pi}{\mathrm{5}}\right)}\:=\:\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\: \\ $$
Commented by cortano1 last updated on 07/Apr/22
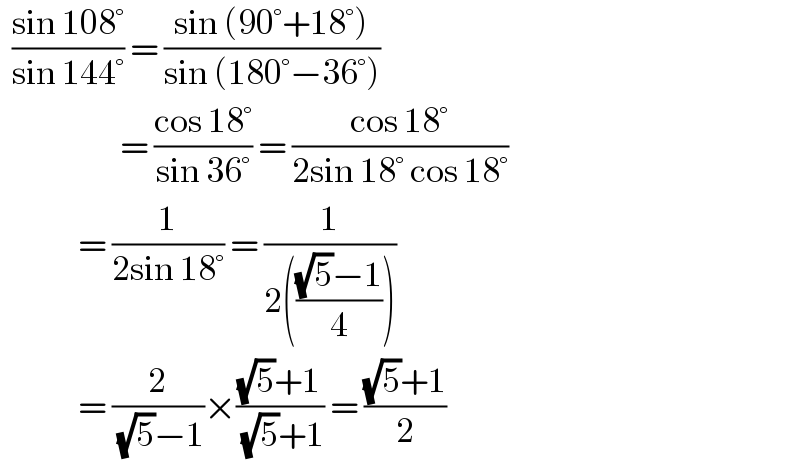
$$\:\:\frac{\mathrm{sin}\:\mathrm{108}°}{\mathrm{sin}\:\mathrm{144}°}\:=\:\frac{\mathrm{sin}\:\left(\mathrm{90}°+\mathrm{18}°\right)}{\mathrm{sin}\:\left(\mathrm{180}°−\mathrm{36}°\right)} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{cos}\:\mathrm{18}°}{\mathrm{sin}\:\mathrm{36}°}\:=\:\frac{\mathrm{cos}\:\mathrm{18}°}{\mathrm{2sin}\:\mathrm{18}°\:\mathrm{cos}\:\mathrm{18}°} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{1}}{\mathrm{2sin}\:\mathrm{18}°}\:=\:\frac{\mathrm{1}}{\mathrm{2}\left(\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{4}}\right)} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}−\mathrm{1}}×\frac{\sqrt{\mathrm{5}}+\mathrm{1}}{\:\sqrt{\mathrm{5}}+\mathrm{1}}\:=\:\frac{\sqrt{\mathrm{5}}+\mathrm{1}}{\mathrm{2}} \\ $$
