Menu Close

prove-that-sin-n-x-dx-p-n-p-2-1-n-cos-x-sin-n-1-x-p-1-sin-n-2-x-dx-

Tinku Tara 0 Comments
Pin




Question Number 63566 by aliesam last updated on 05/Jul/19
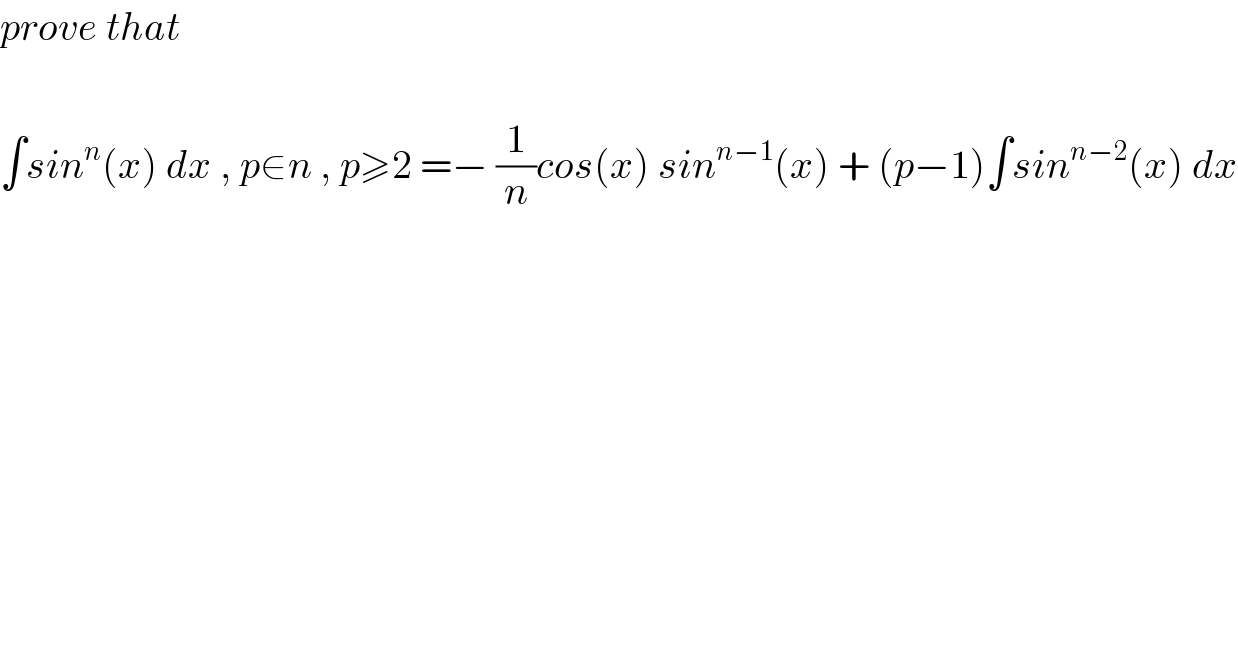
prove that ∫sin^n (x) dx , p∈n , p≥2 =− (1/n)cos(x) sin^(n−1) (x) + (p−1)∫sin^(n−2) (x) dx
provethat∫sinn(x)dx,p∈n,p⩾2=−1ncos(x)sinn−1(x)+(p−1)∫sinn−2(x)dx
Commented by aliesam last updated on 05/Jul/19
thats right it was a typo
thatsrightitwasatypo
Commented by MJS last updated on 05/Jul/19
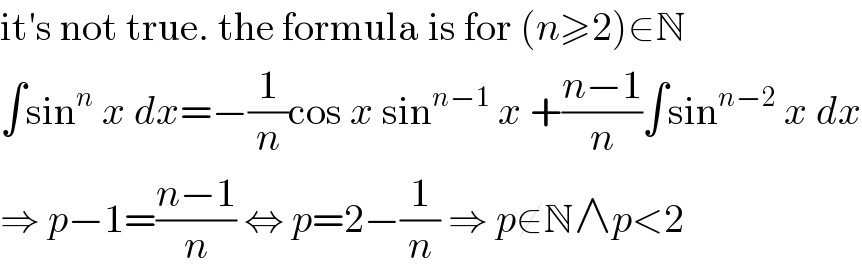
it′s not true. the formula is for (n≥2)∈N ∫sin^n x dx=−(1/n)cos x sin^(n−1) x +((n−1)/n)∫sin^(n−2) x dx ⇒ p−1=((n−1)/n) ⇔ p=2−(1/n) ⇒ p∉N∧p<2
it′snottrue.theformulaisfor(n⩾2)∈N∫sinnxdx=−1ncosxsinn−1x+n−1n∫sinn−2xdx⇒p−1=n−1n⇔p=2−1n⇒p∉N∧p<2

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *