Question Number 87424 by Rio Michael last updated on 04/Apr/20
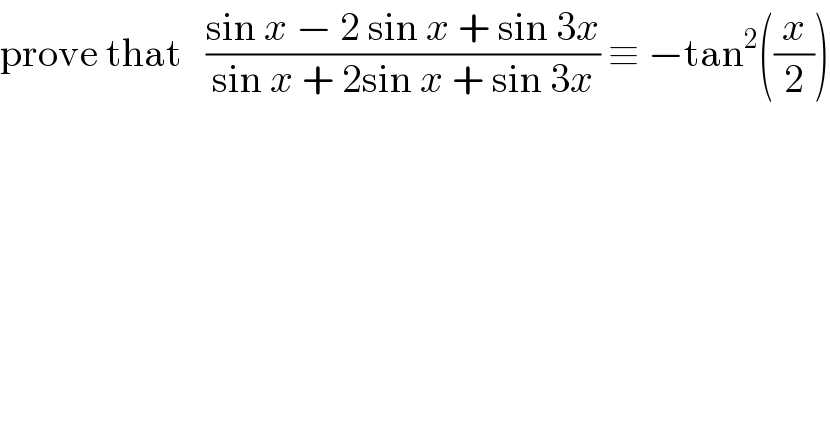
$$\mathrm{prove}\:\mathrm{that}\:\:\:\frac{\mathrm{sin}\:{x}\:−\:\mathrm{2}\:\mathrm{sin}\:{x}\:+\:\mathrm{sin}\:\mathrm{3}{x}}{\mathrm{sin}\:{x}\:+\:\mathrm{2sin}\:{x}\:+\:\mathrm{sin}\:\mathrm{3}{x}}\:\equiv\:−\mathrm{tan}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right) \\ $$
Commented by john santu last updated on 04/Apr/20
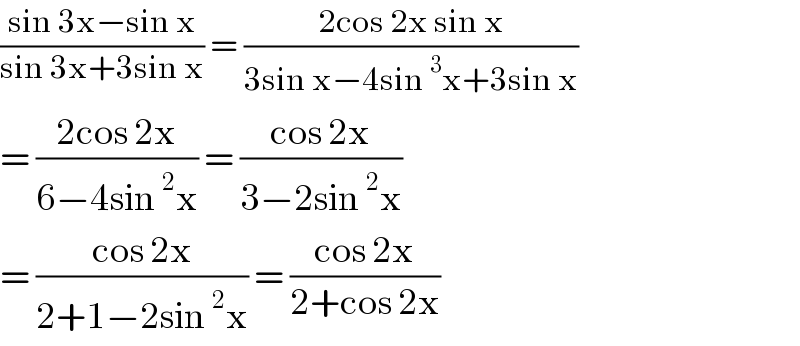
$$\frac{\mathrm{sin}\:\mathrm{3x}−\mathrm{sin}\:\mathrm{x}}{\mathrm{sin}\:\mathrm{3x}+\mathrm{3sin}\:\mathrm{x}}\:=\:\frac{\mathrm{2cos}\:\mathrm{2x}\:\mathrm{sin}\:\mathrm{x}}{\mathrm{3sin}\:\mathrm{x}−\mathrm{4sin}\:^{\mathrm{3}} \mathrm{x}+\mathrm{3sin}\:\mathrm{x}} \\ $$$$=\:\frac{\mathrm{2cos}\:\mathrm{2x}}{\mathrm{6}−\mathrm{4sin}\:^{\mathrm{2}} \mathrm{x}}\:=\:\frac{\mathrm{cos}\:\mathrm{2x}}{\mathrm{3}−\mathrm{2sin}\:^{\mathrm{2}} \mathrm{x}} \\ $$$$=\:\frac{\mathrm{cos}\:\mathrm{2x}}{\mathrm{2}+\mathrm{1}−\mathrm{2sin}\:^{\mathrm{2}} \mathrm{x}}\:=\:\frac{\mathrm{cos}\:\mathrm{2x}}{\mathrm{2}+\mathrm{cos}\:\mathrm{2x}} \\ $$
Commented by john santu last updated on 04/Apr/20
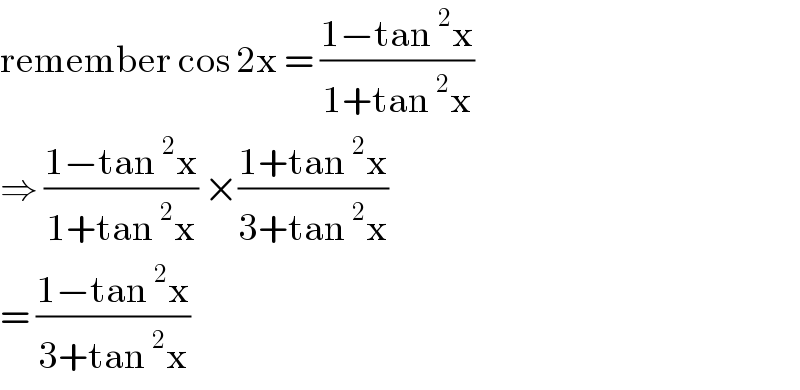
$$\mathrm{remember}\:\mathrm{cos}\:\mathrm{2x}\:=\:\frac{\mathrm{1}−\mathrm{tan}\:^{\mathrm{2}} \mathrm{x}}{\mathrm{1}+\mathrm{tan}\:^{\mathrm{2}} \mathrm{x}} \\ $$$$\Rightarrow\:\frac{\mathrm{1}−\mathrm{tan}\:^{\mathrm{2}} \mathrm{x}}{\mathrm{1}+\mathrm{tan}\:^{\mathrm{2}} \mathrm{x}}\:×\frac{\mathrm{1}+\mathrm{tan}\:^{\mathrm{2}} \mathrm{x}}{\mathrm{3}+\mathrm{tan}\:^{\mathrm{2}} \mathrm{x}}\: \\ $$$$=\:\frac{\mathrm{1}−\mathrm{tan}\:^{\mathrm{2}} \mathrm{x}}{\mathrm{3}+\mathrm{tan}\:^{\mathrm{2}} \mathrm{x}} \\ $$
Commented by Rio Michael last updated on 04/Apr/20

$$\mathrm{okay}\:\mathrm{sir}\:\mathrm{thanks} \\ $$
Commented by Rio Michael last updated on 04/Apr/20
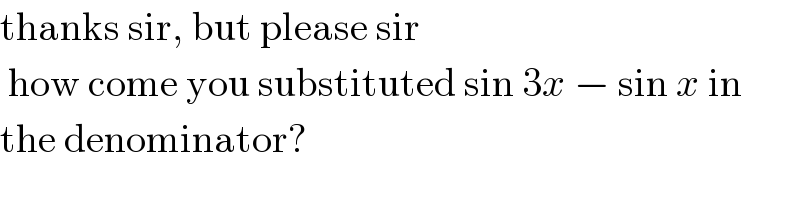
$$\mathrm{thanks}\:\mathrm{sir},\:\mathrm{but}\:\mathrm{please}\:\mathrm{sir}\: \\ $$$$\:\mathrm{how}\:\mathrm{come}\:\mathrm{you}\:\mathrm{substituted}\:\mathrm{sin}\:\mathrm{3}{x}\:−\:\mathrm{sin}\:{x}\:\mathrm{in}\: \\ $$$$\mathrm{the}\:\mathrm{denominator}? \\ $$
Commented by john santu last updated on 04/Apr/20

$$\mathrm{oo}\:\mathrm{sorry}.\:\mathrm{i}\:\mathrm{misread} \\ $$
Answered by Ar Brandon last updated on 04/Apr/20
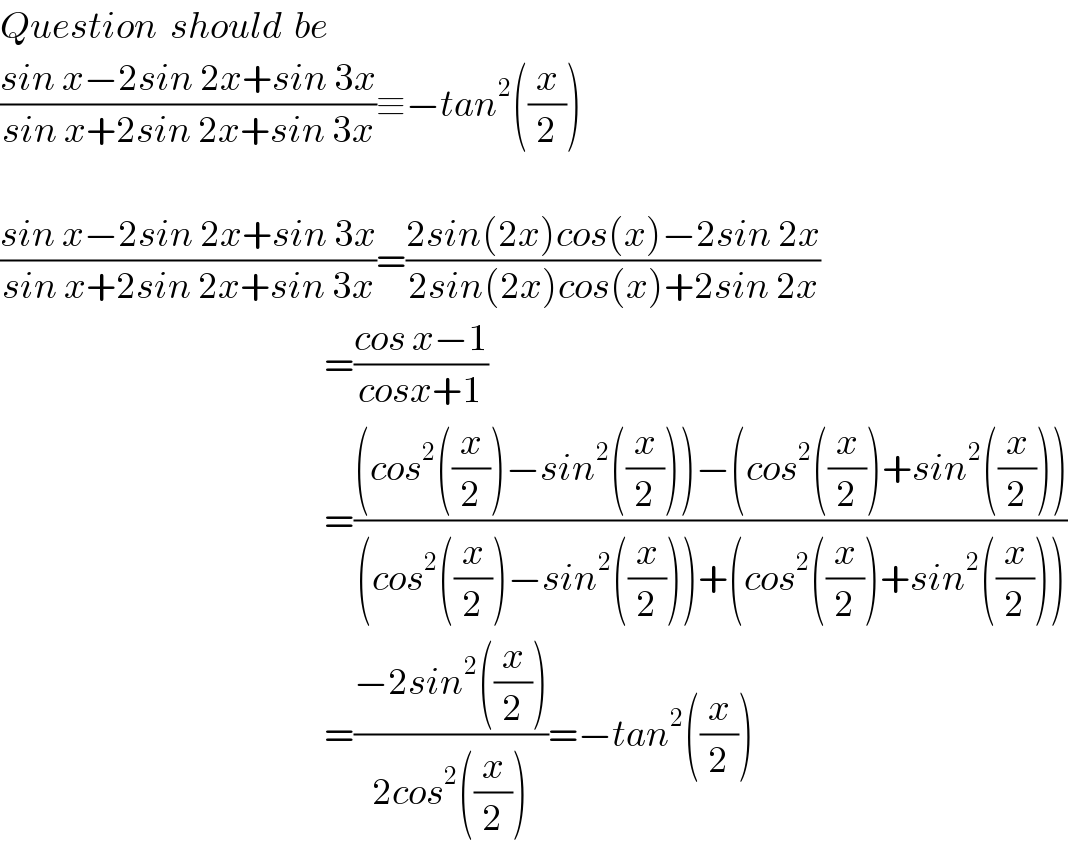
$${Question}\:\:{should}\:\:{be} \\ $$$$\frac{{sin}\:{x}−\mathrm{2}{sin}\:\mathrm{2}{x}+{sin}\:\mathrm{3}{x}}{{sin}\:{x}+\mathrm{2}{sin}\:\mathrm{2}{x}+{sin}\:\mathrm{3}{x}}\equiv−{tan}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right) \\ $$$$ \\ $$$$\frac{{sin}\:{x}−\mathrm{2}{sin}\:\mathrm{2}{x}+{sin}\:\mathrm{3}{x}}{{sin}\:{x}+\mathrm{2}{sin}\:\mathrm{2}{x}+{sin}\:\mathrm{3}{x}}=\frac{\mathrm{2}{sin}\left(\mathrm{2}{x}\right){cos}\left({x}\right)−\mathrm{2}{sin}\:\mathrm{2}{x}}{\mathrm{2}{sin}\left(\mathrm{2}{x}\right){cos}\left({x}\right)+\mathrm{2}{sin}\:\mathrm{2}{x}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{{cos}\:{x}−\mathrm{1}}{{cosx}+\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\left({cos}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)−{sin}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)\right)−\left({cos}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)+{sin}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)\right)}{\left({cos}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)−{sin}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)\right)+\left({cos}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)+{sin}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)\right)} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{−\mathrm{2}{sin}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)}{\mathrm{2}{cos}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)}=−{tan}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right) \\ $$
Commented by Rio Michael last updated on 04/Apr/20
$$\mathrm{thanks}\:\mathrm{bro},\mathrm{for}\:\mathrm{the}\:\mathrm{correction} \\ $$
Commented by Ar Brandon last updated on 04/Apr/20
��
