Prove-that-sinh-1-tan-log-tan-2-pi-4-Mastermind-

Question Number 168187 by Mastermind last updated on 05/Apr/22

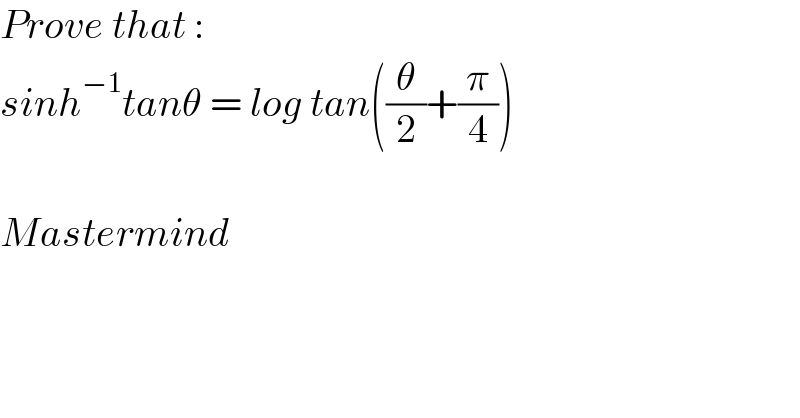
Prove that : sinh^(−1) tanθ = log tan((θ/2)+(π/4)) Mastermind

$${Prove}\:{that}\::\: \\ $$$${sinh}^{−\mathrm{1}} {tan}\theta\:=\:{log}\:{tan}\left(\frac{\theta}{\mathrm{2}}+\frac{\pi}{\mathrm{4}}\right) \\ $$$$ \\ $$$${Mastermind} \\ $$

Answered by peter frank last updated on 06/Apr/22

sinh^(−1) x=ln (x+(√(x^2 −1)) ) x=tan θ sinh^(−1) tan θ=ln (tan θ+sec θ) ln (tan θ+sec θ)=ln (((1+sin θ)/(cos θ))) ln (((1+sin θ)/(cos θ)))=ln (((cos (θ/2)+sin (θ/2))^2 )/(cos^2 (θ/2)−sin^2 (θ/2))) =ln (((1+tan (θ/2))/(1−tan (θ/2))))=ln[ tan ((π/4)+(θ/2))] sinh^(−1) tan θ=lntan [ ((π/4)+(θ/2))]

$$\mathrm{sinh}\:^{−\mathrm{1}} \mathrm{x}=\mathrm{ln}\:\left(\mathrm{x}+\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}\:\right) \\ $$$$\mathrm{x}=\mathrm{tan}\:\theta \\ $$$$\mathrm{sinh}\:^{−\mathrm{1}} \mathrm{tan}\:\theta=\mathrm{ln}\:\left(\mathrm{tan}\:\theta+\mathrm{sec}\:\theta\right) \\ $$$$\mathrm{ln}\:\left(\mathrm{tan}\:\theta+\mathrm{sec}\:\theta\right)=\mathrm{ln}\:\left(\frac{\mathrm{1}+\mathrm{sin}\:\theta}{\mathrm{cos}\:\theta}\right) \\ $$$$\mathrm{ln}\:\left(\frac{\mathrm{1}+\mathrm{sin}\:\theta}{\mathrm{cos}\:\theta}\right)=\mathrm{ln}\:\frac{\left(\mathrm{cos}\:\frac{\theta}{\mathrm{2}}+\mathrm{sin}\:\frac{\theta}{\mathrm{2}}\right)^{\mathrm{2}} }{\mathrm{cos}^{\mathrm{2}} \:\frac{\theta}{\mathrm{2}}−\mathrm{sin}\:^{\mathrm{2}} \frac{\theta}{\mathrm{2}}} \\ $$$$=\mathrm{ln}\:\left(\frac{\mathrm{1}+\mathrm{tan}\:\frac{\theta}{\mathrm{2}}}{\mathrm{1}−\mathrm{tan}\:\frac{\theta}{\mathrm{2}}}\right)=\mathrm{ln}\left[\:\mathrm{tan}\:\left(\frac{\pi}{\mathrm{4}}+\frac{\theta}{\mathrm{2}}\right)\right] \\ $$$$\mathrm{sinh}\:^{−\mathrm{1}} \mathrm{tan}\:\theta=\mathrm{lntan}\:\left[\:\left(\frac{\pi}{\mathrm{4}}+\frac{\theta}{\mathrm{2}}\right)\right] \\ $$$$ \\ $$

Commented by Mastermind last updated on 07/Apr/22

$${Thanks} \\ $$

Answered by Mathspace last updated on 05/Apr/22

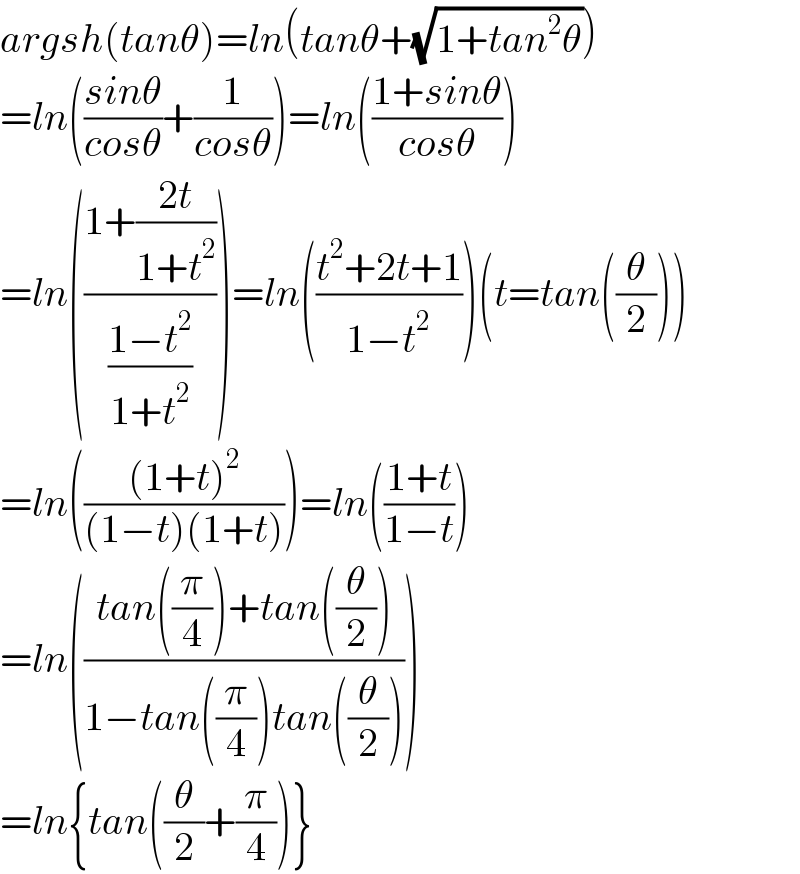
argsh(tanθ)=ln(tanθ+(√(1+tan^2 θ))) =ln(((sinθ)/(cosθ))+(1/(cosθ)))=ln(((1+sinθ)/(cosθ))) =ln(((1+((2t)/(1+t^2 )))/((1−t^2 )/(1+t^2 ))))=ln(((t^2 +2t+1)/(1−t^2 )))(t=tan((θ/2))) =ln((((1+t)^2 )/((1−t)(1+t))))=ln(((1+t)/(1−t))) =ln(((tan((π/4))+tan((θ/2)))/(1−tan((π/4))tan((θ/2))))) =ln{tan((θ/2)+(π/4))}

$${argsh}\left({tan}\theta\right)={ln}\left({tan}\theta+\sqrt{\mathrm{1}+{tan}^{\mathrm{2}} \theta}\right) \\ $$$$={ln}\left(\frac{{sin}\theta}{{cos}\theta}+\frac{\mathrm{1}}{{cos}\theta}\right)={ln}\left(\frac{\mathrm{1}+{sin}\theta}{{cos}\theta}\right) \\ $$$$={ln}\left(\frac{\mathrm{1}+\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }}{\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }}\right)={ln}\left(\frac{{t}^{\mathrm{2}} +\mathrm{2}{t}+\mathrm{1}}{\mathrm{1}−{t}^{\mathrm{2}} }\right)\left({t}={tan}\left(\frac{\theta}{\mathrm{2}}\right)\right) \\ $$$$={ln}\left(\frac{\left(\mathrm{1}+{t}\right)^{\mathrm{2}} }{\left(\mathrm{1}−{t}\right)\left(\mathrm{1}+{t}\right)}\right)={ln}\left(\frac{\mathrm{1}+{t}}{\mathrm{1}−{t}}\right) \\ $$$$={ln}\left(\frac{{tan}\left(\frac{\pi}{\mathrm{4}}\right)+{tan}\left(\frac{\theta}{\mathrm{2}}\right)}{\mathrm{1}−{tan}\left(\frac{\pi}{\mathrm{4}}\right){tan}\left(\frac{\theta}{\mathrm{2}}\right)}\right) \\ $$$$={ln}\left\{{tan}\left(\frac{\theta}{\mathrm{2}}+\frac{\pi}{\mathrm{4}}\right)\right\} \\ $$

Commented by Mastermind last updated on 07/Apr/22

$$ \\ $$$${Thanks} \\ $$

Facebook Tweet Pin

Prove-that-sinh-1-tan-log-tan-2-pi-4-Mastermind-

Leave a Reply Cancel reply